7.5 Writing Recursive Functions: Using a Set of Test Scenarios

A variation on the approach we just saw is to think in terms of a set of scenarios. We’ll record these in a table, with one row for each scenario, as you would if you were designing a test suite. Ultimately, we will think through a thorough set of scenarios, but we can start with just those that are suggested by the recursive structure of the problem.

Here is our design recipe:

1. Create one row in the table for each scenario suggested by the recursive structure of the problem.

2. For each case that is so simple that no recursion is called for, write down what the function should do (what it should return and/or mutate).

3. For each case that is complex enough that one or more recursive calls will help:

   • Write down what recursive call(s) should be made, and use the docstring of the function to determine what each will do (what it will return and/or mutate).

   • Write down what the present call needs to do with those results to accomplish its goal.

4. Add to the table any other scenario(s) that you feel are important to think through, along with a concrete example. For each,

   • If it can be handled using the strategy of any previous scenario, record that fact. We won’t need code for this specific case!

   • If not, handle the novel scenario as per steps (2) and (3) above.

As an example, suppose we want to design this function:

def flatten(obj: int | list) -> list[int]:
    """Return a (non-nested) list of the integers in <obj>.

    The integers are returned in the left-to-right order they appear
    in <obj>.
    """

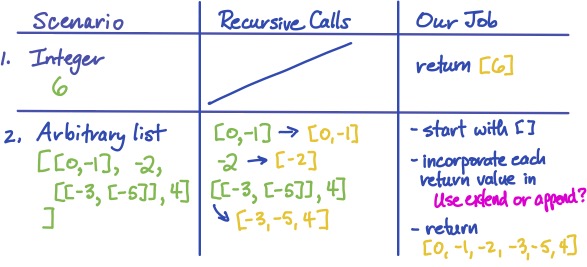
As suggested by the recursive structure of a nested list, our first two scenarios are a simple integer and a list containing nested sublists. We pick an arbitrary example of each:

In scenario 1, the problem is so easy that we don’t need any “help” from a recursive call. We can simply put the given integer into a list and return that. It’s easy to see that this strategy would work for any integer. We record this strategy in the table:

For scenario 2, we have chosen an non-trivial example of a list input. This will help us to ensure our solution in this case is as general as possible, in other words, that it will handle lots of different list inputs. First, we write down the recursive call(s) that should be made. Since this is a list of nested lists, all of which could contribute to the result for flatten, we will need to recurse on each of them. Then we use the docstring of the function to determine what each will do (what it will return and/or mutate). We record this in the middle column of the table:

Assuming each recursive call works properly, what does our call have to do in order to return the correct answer? It’s fairly easy to see that we need to put those individual results together into a single list and return it. We can start out with an empty list, and after each recursive call, add in its result. (We’ll need to think about whether append or extend is the right list method to use, but that is a minor detail.) We record this in the third column:

We might think of a couple of additional scenarios, as shown here:

The empty list, however, is already handled by our solution to scenario 2. In this case, we’ll start with an empty list, iterate 0 times, and return that empty list—which is correct! Thinking through an example of a list of integers, we can see that this is also already handled by scenario 2! Here is our complete table of scenarios, with these observations included:

When we translate our analysis into code, we’ll only need to implement the first two rows. With all of our previous work, doing so is quite simple:

def flatten(obj: Union[int, list]) -> List[int]:
    """Return a (non-nested) list of the integers in <obj>.

    The integers are returned in the left-to-right order they appear
    in <obj>.
    """
    if isinstance(obj, int):
        return [obj]
    else:
        s = []
        for sublist in obj:
            s.extend(flatten(sublist))
        return s

Then to test our code, we can take advantage of all four scenarios to check that our function works correctly. If our reasoning was correct, all tests will pass successfully. The purpose of testing them anyway is to check that reasoning! Here we can see that our function indeed works correctly in all four scenarios:

>>> flatten(6)
[6]
>>> flatten([[0, -1], -2, [[-3, [-5]], 4]])
[0, -1, -2, -3, -5, 4]
>>> flatten([])
[]
>>> flatten([8, 13, -2])
[8, 13, -2]

An interesting question is how we should record these tests. Should they be doctests or unit tests run with pytest? Remembering that the purpose of doctests is to communicate to the reader what the correct behaviour of the function looks like, we might put only the first two scenarios into doctests. The rest are better suited to unit tests in a separate file, where we do our most thorough testing.