8.7 Tree Traversals

We’ve seen several methods that travel through, or “traverse” a tree. Some visit every value in the tree (e.g., Tree.__str__), while others don’t have to (e.g., BinarySearchTree.__contains__). Another way in which these methods vary is when they deal with a node vs. when they deal with its subtrees.

Pre-order and post-order

Consider Tree.__str__. The real work happens in its helper method:

def _str_indented(self, depth: int) -> str:
    """Return an indented string representation of this tree.

    The indentation level is specified by the <depth> parameter.
    """
    if self.is_empty():
        return ''
    else:
        s = '  ' * depth + str(self._root) + '\n'
        for subtree in self._subtrees:
            s += subtree._str_indented(depth + 1)
        return s

Here, “dealing with” the root means adding its value in to the string that will be returned. We chose to do this before dealing with its subtrees. As a result, the root is the very first thing in the resulting string. Since the method is recursive, the same is true within each subtree: each root appears before its subtrees, as we saw earlier:

>>> t1 = Tree(1, [])
>>> t2 = Tree(2, [])
>>> t3 = Tree(3, [])
>>> t4 = Tree(4, [t1, t2, t3])
>>> t5 = Tree(5, [])
>>> t6 = Tree(6, [t4, t5])
6
  4
    1
    2
    3
  5

This is called a pre-order traversal because we deal with the root before (or “pre”) its subtrees.

With a simple change to the code, we can instead add the root’s value in to the string after adding its subtrees:

def _str_indented(self, depth: int) -> str:
    """Return an indented string representation of this tree.

    The indentation level is specified by the <depth> parameter.
    """
    if self.is_empty():
        return ''
    else:
        s = ''  # We still need to initialize s.
        for subtree in self._subtrees:
            s += subtree._str_indented(depth + 1)
        s = s + '  ' * depth + str(self._root) + '\n'  # Add the root in.
        return s

Now the output for that same tree has each root after its subtrees:

    1
    2
    3
  4
  5
6

This is called a post-order traversal because we deal with the root after (or “post”) its subtrees.

Sometimes it matters whether we use pre-order or post-order

In the example above, it didn’t matter whether we chose pre-order or post-order traversal (unless we cared which form the output would take); either way, the tree is displayed. But for other methods, we don’t have a choice.

Recall BinarySearchTree.__contains__:

def __contains__(self, item: Any) -> bool:
    """Return whether <item> is in this BST.
    """
    if self.is_empty():
        return False
    elif item == self._root:
        return True
    elif item < self._root:
        return item in self._left   # or, self._left.__contains__(item)
    else:
        return item in self._right  # or, self._right.__contains__(item)

For this method, “dealing with” a node means comparing its root with item. In the code above, we look at the root before recursing on a subtree. If we didn’t do that, we would not know which subtree(s) item might occur in, and would be forced to look in both. While we could write the method using post-order traversal, it would be unnecessarily inefficient. The only way to get the benefit of the ordered nature of the BST is to deal with the root before dealing with its children. So we use pre-order traversal.

Here’s a great example of the opposite situation, where we are forced to use post-order traversal. We can use a tree to represent an arithmetic expression. The root is an operator, and its subtrees are the operands. Here’s a simple tree that represents the expression 18 * 4:

You know, of course, that operands can themselves be expressions. Our tree representation easily handles this. Here’s a bigger example:

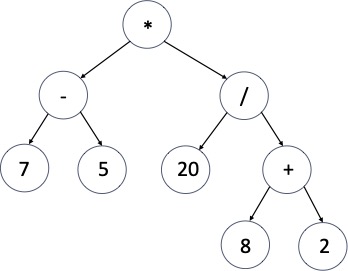
Do you see how it represents the arithmetic expression \((7 - 5) \times (20 / (8 + 2))\)? Now think about a method whose job is to return the value of the expression represented by a tree. It couldn’t apply the operation stored in the root (multiply, add, or whatever) until after determining the value of each subtree—recursively, of course. So this method must do a post-order traversal.

You’ll see the code for evaluating an expression tree later in this chapter.

With binary trees, there is another option

So far, we’ve either dealt with the root before its subtrees or after its subtrees. With a binary tree, there are only two children (at most). This opens up the option of dealing with the root in between dealing with its left subtree and dealing with its right subtree. This is called in-order traversal.

Suppose we want to write a BST method that returns a list of the contents of the BST, in non-decreasing order. Here we do it using an in-order traversal:

def to_sorted_list(self) -> list:
    """Return a list of this BST's items in non-decreasing order.
    """
    if self.is_empty():
        return []
    else:
        # Deal with the root (i.e., add its value to the list we are building) in between
        # dealing with its subtrees.
        return self._left.to_sorted_list() + [self._root] + self._right.to_sorted_list()

In the recursive case, if the two recursive calls does what the docstring says, they will each return a list of items in non-decreasing order. Further, the BST property says that the root is greater than or equal to all items in its left subtree, and less than or equal to all items in its right subtree. These facts guarantee that the list returned is in non-decreasing order even though we did not sort it! This example demonstrates:

>>> left = BinarySearchTree(6)
>>> left._left = BinarySearchTree(2)
>>> left._right = BinarySearchTree(8)
>>> left._right._left = BinarySearchTree(7)
>>> right = BinarySearchTree(20)
>>> right._right = BinarySearchTree(30)
>>> bst = BinarySearchTree(10)
>>> bst._left = left
>>> bst._right = right
>>> print(bst.to_sorted_list())
[2, 6, 7, 8, 10, 20, 30]

The only way to get the values in sorted order without doing any extra work is to use in-order traversal. How would we change the method if we wanted the list to be in non-increasing order?

Of course, if this method were written for an ordinary binary tree class, then doing an in-order traversal would guarantee nothing about the order of the output.

Item order

To check your understanding of the traversal orders, we often ask you to write out the pre-order, in-order, or post-order traversal of a tree. The easiest way to do this is to think recursively. And it requires no memorization—other than to remember what “pre” and “post” mean.

Here’s a general tree with values in no particular order:

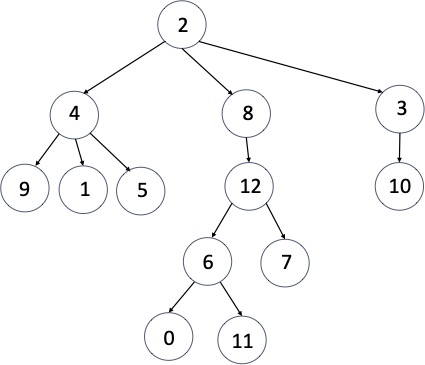
If we are writing its post-order traversal, we know the root has to come last and its subtrees come beforehand. So we can write that much down, leaving space for each of its three subtrees (strategically, we have left more space for larger subtrees):

We can easily use the same strategy for the first subtree and the last subtree, since they are so simple:

The middle subtree is bigger, so it takes a little more work, but the strategy holds. In the end, we get this:

We would do a pre-order traversal with the same strategy, except that the root comes first:

In the end, we would have this:

Here’s a binary tree so we can do an in-order traversal. It’s not a BST though—that would be too easy!

We use the same strategy, except of course the root is in between its children.

Try completing this traversal yourself. This is the final answer: