7.7 Recursion and the call stack

The key to partial tracing is that we don’t trace into the recursive calls. We’ve learned that we don’t have to, because an inductive argument demonstrates that partial tracing is sufficient. But when your code is actually run, each recursive call (like all calls) creates a stack frame that is pushed. And each return (like all returns) pops the top stack frame. Of course one recursive call may make other recursive calls, and they may do the same. Python keeps track of all of this on the call stack.

Let’s do one small example to see what Python takes care of for us. Rather than look at our old favourite, sum_nested, let’s start with something even simpler:

def sum_ordinary(lst: list[int]) -> int:
    """Return the sum of the numbers in ordinary (non-nested) list <lst>.

    >>> sum_ordinary([])
    0
    >>> sum_ordinary([5, 1, 3, 9])
    18
    """
    if len(lst) == 0:
        return 0
    else:
        sum_of_rest = sum_ordinary(lst[1:])
        total = lst[0] + sum_of_rest
        return total

This is a function we don’t need to write because the built-in sum function does the same thing, but it is a good example to illustrate how the call stack works with a recursive function. You’ll notice that we have split what could easily be a one-line else-block into three lines. This also is for illustrative purposes.

Now watch this video to see how the recursion unfolds.

For a list of length 4, a total of 5 calls to the function are made: the initial call with the list of length 4, a call with a list of length 3, one with a list of length 2, one with a list of length 1, and, finally, one with a list of length 0. So 5 stack frames are generated in total, plus one for the main block where everything started. We confirmed this in the video, when we saw that the stack peaked in size the moment it had those 6 frames.

There’s one interesting detail that the debugger doesn’t highlight. The argument to the recursive call is not made by mutating lst. Instead, our function uses the slice operator. Recall that slicing always creates a new list object. And that new list is a “shallow copy” of the old list: it’s a new list, but it contains the same ids (for whichever list elements we kept when slicing) as in the old list. We don’t get new copies of the objects that the ids refer to.

So: every time sum_ordinary recurses, a new list object is created. Here’s how it looks in the memory model when we reach the call to sum_ordinary with a list of length 0 (the empty list):

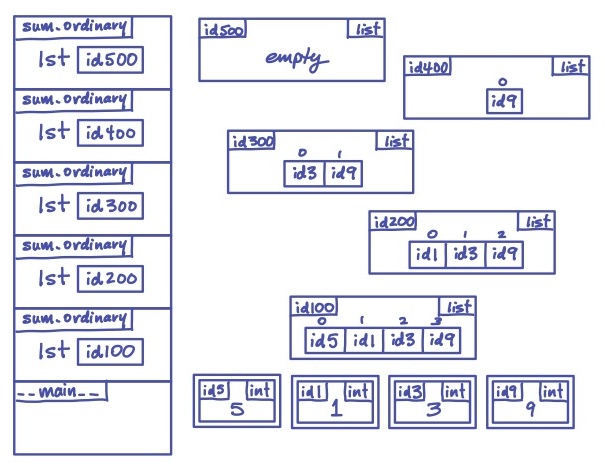
(We chose id values that are conveniently the same as the ints they refer to.)

For comparison, here’s what the debugger shows us at the same moment:

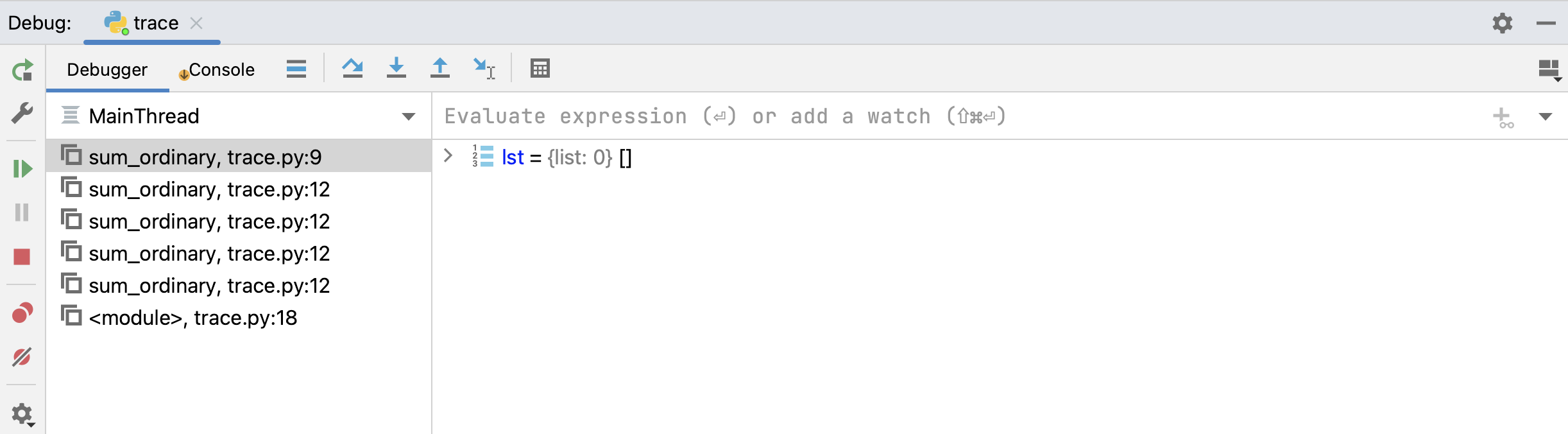
We see the stack frames on the left, and the variables that exist in the top stack frame (the one we are currently executing) on the right, in this case, the parameter lst which currently is an empty list. As we saw in the video, we can click on any of the other stack frames to see their variables. Here’s we’ve clicked several frames down in the stack, when lst had three elements:

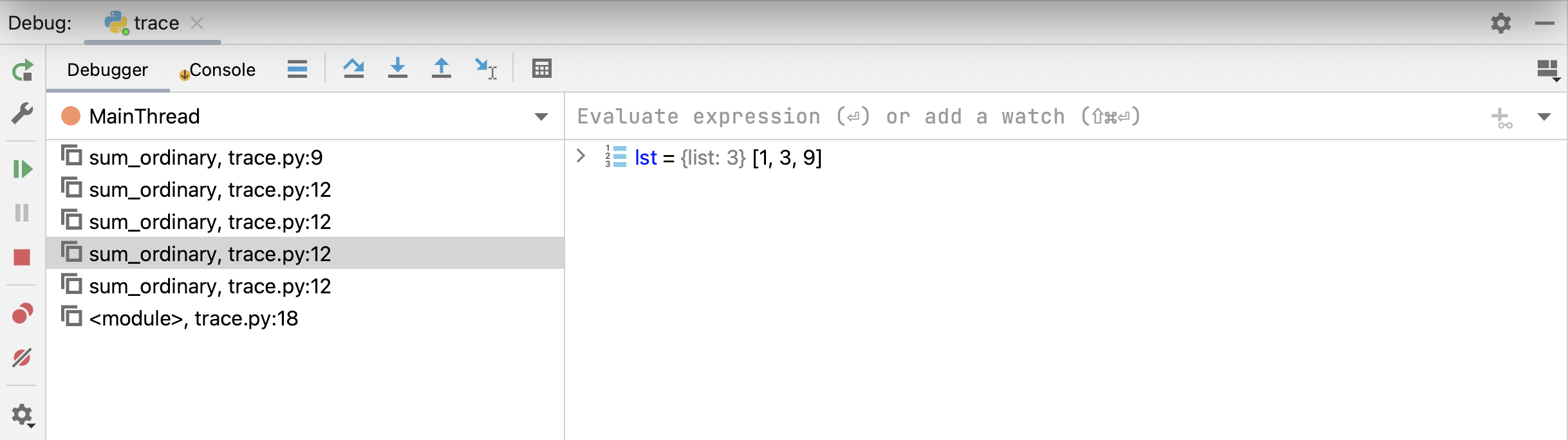
You could believe that there is one variable called lst that is changing. But there is not just one! Every call to sum_ordinary has its own parameter lst sitting inside its own stack frame, as we see in the full memory model diagram above. At that moment in time, there are five different variables called lst on the call stack.

Linear recursion

Notice that, with function sum_ordinary, a call to the function either doesn’t recurse at all or makes a single recursive call. This is called linear recursion, because it leads to a linear sequence of recursive calls (and a fairly simple set of actions on the call stack).

Recursive code that is linear can usually be translated into iterative code that is no more complicated. For example, we can rewrite sum_ordinary with a very simple loop:

def sum_ordinary(lst: list[int]) -> int:
    """Return the sum of the numbers in ordinary (non-nested) list <lst>.

    >>> sum_ordinary([])
    0
    >>> sum_ordinary([5, 1, 3, 9])
    18
    """
    total = 0
    for item in lst:
        total += item
    return total

If this was the whole story of recursion, there wouldn’t be much motivation for learning it. But when we get beyond linear recursion, we can write elegant code that does not have an iterative equivalent that is as simple.