Hash index
CSC443 Article
1. Introduction
In this article, we continue with the discussion on disk based indexing techniques for speeding up record lookup.
Recall B+ trees is an adaptation of balanced sorted trees to secondary storage devices. We are going to present several disk based adaptions of hash tables, and so that the idea of hashing is a powerful tool for highly efficient data lookups on disk.
2. Simple disk based hash table
The simple disk based hash table is a straight forward adaptation of main memory hash table to secondary storage devices.
Let
The disk hash table consists of a data file
Furthermore, let
A simple hash table on disk is completely characterized by:
- a number
$N$ of buckets. - a hash function
$h: \mathcal{K} \to N$
The hash function maps key values to an integer$0\leq h(k) \lt N$ . - a page locating function
$\mathrm{loc}: N\to\mathrm{addr}(\mathrm{Pages}(F))$
The locating function maps an integer$i$ to some page address.
It is understood that both
These hashing methods produce very large integers (e.g. 128-bit). So, we would need to modify the range of these hashing methods using integer modulo:
Efficient implementations of
- Let the data file
$F$ consists of contiguous pages, so we can define:$$\mathrm{loc}(i) = p_0 + i\times B$$ where$p_0$ is the beginning of the data pages on disk,$B$ is the page size. - If
$F$ is a heap file, and the pages are not consecutive aligned on disk, we can build a lookup array$A$ to store the page pointers. The array is bounded by$N$ . Because the array only needs to store page pointers, for many applications, it can be cached in main memory.$$\mathrm{loc}(i) = A[i]$$
The motivation of building a hash table on a data file is to speed up record
lookup by their key. By the functions
When two records have the same hash value, they will be mapped to the same
page. This is called a collision.
When the number of records in the database become large, the number of
collisions will increase, and some pages
The solution is to allow overflow pages
2.1. Insertion
Key get_key(Record); /* Get the key of the record */
long h(Key key); /* Compute the hash value */
PageAddress loc(long hash); /* Locate the page address */
/**
* inserts a record into a disk based `HashTable`
*/
void insert(HashTable t, Record record) {
Key key = get_key(record);
long hash = h(key);
PageAddress page_ptr = loc(hash);
Page page = Disk::read_page(page_ptr);
while(page.isFull()) {
PageAddress page_ptr = page.next;
if(page_ptr == null)
page_ptr = Disk::allocate_page();
page = Disk::read_page(page_ptr);
}
insert_into_page(page, record);
Disk::write_page(page_ptr, page);
}
Go through the linked list starting with loc(hash) until we
find a vacancy for the record.
2.2. Search
/**
* locates all records matching the `key` in the page. The results are
* appended to `results`
*/
void Page::find_records_by_key(Key key, vector<Record> *results);
/**
* Locates all records in a hash table by key
*/
vector<Record> lookup(Hashtable t, Key key) {
long hash = h(key);
PageAddress page_ptr = loc(hash);
if(page_ptr == null) {
return NOT_FOUND;
}
vector<Record> results;
while(page_ptr) {
Page page = Disk::read_page(page_ptr);
page.find_records_by_key(key, &results)
page_ptr = page.next_page;
}
return results
}
loc(hash)locates the first page that may containkey.- we have to iterate through all the pages in the linked list and
look for records matching the given
key.
3. Extensible hash table
Simple hash table suffers from a severer drawback: the disk I/O required is linear to the average length of the linked lists storing the collisions. In order to maintain the constant disk I/O cost that is expected from hash tables, one must guarantee a bounded length for the linked list.
A simple hash table cannot achieve constant record lookup if the number of records keeps growing. The main reasons are:
- a hash table has a fixed
$n$ number of buckets:$\mathrm{hash}(k)\mod n$ . - if
$n$ is too small, the linked lists are long, resulting in an increase in disk I/O. - a change in
$n$ requires one to redistribute all the records in the hash table, which is impractical.
In this section, we introduce a disk based data structure , extensible hash table, based on hash tables to address the problem.
Extensible hash table is also often referred to as extendible hash table.
3.1. Definition of hash tables
Extensible hash table extends the simple hash table in two fundamental ways:
- a directory mapping bit vectors to pages. 2. a scheme that uses variable number of bits of the hash value of a key.
Let
-
an integer counter,
$D$ , known as the global depth of the extensible hash table. -
a table that maps bit vectors of length
$D$ to page addresses. The table has$2^D$ entries for bit vectors "$00\dots0$ " to "$11\dots1$ ". We denote the table by the function$\mathrm{dir}: 2^D \to \mathrm{addr}(\mathrm{Pages}(F))$
Intuitively, given a record
NOTE: it's possible for two bit vectors to be mapped to the same page.
The following data structure represents an extensible hash table.
struct Directory {
int global_depth;
PageAddress table[];
}
We can always assert that
length(Directory.table) $\leq$ pow(2, Directory.global_depth)
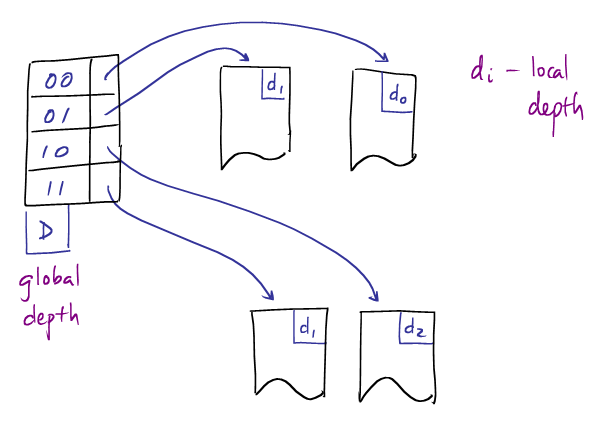
A small extensible hash table with global depth of 2, and 4 pages.
3.2. Looking up in extended hash table
Let a key,
The lookup algorithm for extended hash table is straight forward. To
look up record(s) with key value
- Let
$p = \mathrm{dir}(h(k|D))$ - Read page
$p$ from disk, and search through the page for matching records.
3.3. Resize extensible hash table
The directory structure allows extensible hash table to resize itself
with minimal overhead. Given an extended hash table
Extended hash table can grow its capacity by factor of two with resizing to avoid collisions.
Collision in extended hashing
Though very rare, it's still possible for collisions to occur in extended hashing:
-
two keys,
$k_1$ and$k_2$ , may have the same hash code. Namely,$h(k_1) = h(k_2)$ . Therefore, it's certainly not possible for extended hashing to distinguish them. -
there may be duplicate keys in the data among records.
The resizing is done as follows:
$D_\mathrm{new} = D+1$ $\mathrm{dir}_\mathrm{new}(i) = \mathrm{dir}(i \gg 1)$ where$i \gg 1$ is the bit-shift of$i$ by one bit to the right. In other words,$\mathrm{dir}_\mathrm{new}$ uses only$D$ bits of$i$ .
Lemma:
- for
$0\leq i \lt 2^D$ :$\mathrm{dir}_\mathrm{new}(i) = \mathrm{dir}(i)$ - for
$2^D\leq i \lt 2^{D+1}$ :$\mathrm{dir}_\mathrm{new}(i) = \mathrm{dir}(i-2^D)$
The first half and second half of grow_directory.
void grow_directory(Directory *dir) {
int D = dir->global_depth;
int new_len = pow(2, D+1);
dir->table = (PageAddress *)realloc(sizeof(PageAddress) * new_len);
memcpy(
dir->table+sizeof(PageAddress)*(new_len/2), // destination (second half)
dir->table, // source (first half)
sizeof(PageAddress) * new_len/2)
dir->global_depth ++;
}
This copies the first half into the second half in the table.
We illustrated the algorithm using
memcpy,
assuming that the directory is stored in memory.
Observation
-
After the resizing, the new extended hash table uses
$D+1$ bits to locate the page. It's important to note that the duplication of the first half of$\mathrm{dir}_\mathrm{new}$ in its second half ensures that all records that can be located using$D$ bits can also be located using$D+1$ bits from their hash values. -
Resizing does not need to touch the pages, so it can be very efficiently implemented even if the directory is stored on disk.
3.4. Insert into extensible hash table
Recall, we indicated that each page must have a counter, the local depth, that indicates the number of bits used to hash its records. The local depth was not used for lookup, but it becomes crucial for insertion and dynamic hashing.
Inserting a record into an extensible hash table involves the following steps.
-
Given a record with some key value,
$k$ , we locate the page that using$\mathrm{dir}[h(k|D)]$ . If the page has vacancy, insert the record in that page. -
If the page
$p$ is full, we need to split the page to two or more pages. This is done by distinguishing the records in$p$ by more bits than its current local depth. Each pages after the split will have a greater local depth, and fewer records hashed to it. If the new local depth exceeds the global depth, we also keep the grow the directory. Finally, the directory table needs to be updated so the split pages are references by the correct table entries.
The following algorithm describes these steps in detail.
void insert(Directory &dir, Record r_new) {
/**
* locate the page that _should_ contain `r_new`
*/
Key key = get_key(r_new)
Page p = lookup(dir, key)
/**
* if there is vacancy for one more record, then insert, and
* we are done.
*/
if p has vacancy {
p.add(r_new);
}
/**
* page splitting is needed to create vacancy in the
* extended hash table.
*/
else {
// gather all the records we need to relocate in `all_records`
// gather all their respective keys in `all_keys`
vector<Record> all_records = get_records(p) $\cup$ {r_new}
vector<BitVector> all_keys = {get_key($x$) : $x\in$ all_records};
// make sure we choose a local_depth large enough
// to distinguish the records. This ensures that the
// split pages will not be full.
int d = longest_common_prefix(all_keys) + 1;
// grow the directory if necessary
while(dir->global_depth < d) {
grow_directory(dir);
}
// get the number of distinct hash values of length d-bits.
// This is the number of pages we need.
vector<BitVector> distinct_hash = {$h$($k$|$d$) : $k\in$ all_keys}
foreach(BitVector j $\in$ distinct_keys) {
// create a new page for each d-bit hash value,
// and move all the records with such hash value
// to this page.
Page p_new = allocate_new();
p_new.local_depth = d;
p_new.add({$x\in$ all_keys : h(get_key($x$)|d) == j});
// update the directory table, so the D-bit hash values
// are mapped to the right page address
$D$ = dir->global_depth
if($D$ > d)
for(BitVector padding=0; padding < pow(2, D-d); padding ++) {
j2 = BitVector::concatenate(j, padding)
dir->table[j2] = get_address(p_new);
}
else
dir->table[j] = get_address(p_new);
}
}
}
Example
| Consider an extensible hash table as shown. It's global depth is 1, with two pages and three records. | 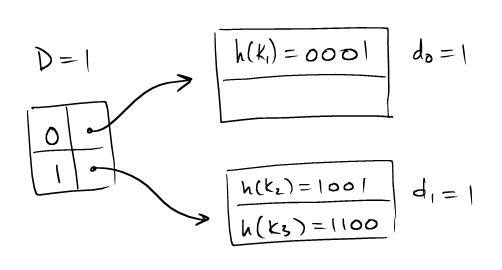 |
| If we are to grow it once, the global depth will be 2. While there are still two pages, the new directory can now index up to four pages. | 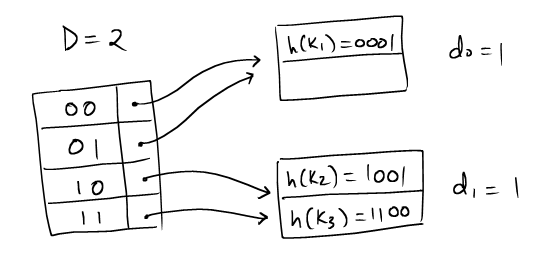 |
| Suppose that we are trying to insert a records with $k_3$ such that the hash value is $h(k_3) = 1010$. We are to first locate the page to insert the record into. | 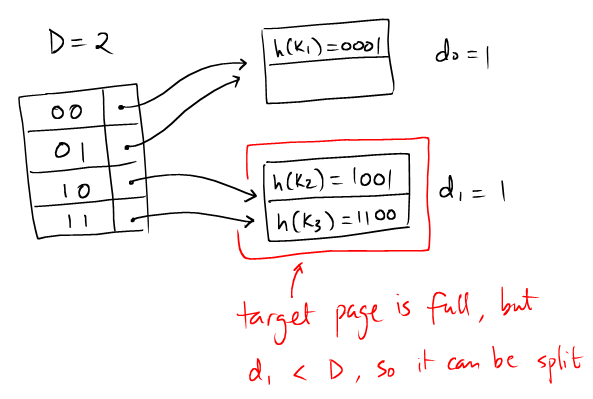 |
|
Since the page is full, we need to split the page. The keys of the records are:
One can observe that the common prefix is 1, so the new local depth must be 2. The records are to be distributed according to the first two bits of their hash values:
Finally, we need to update the directory table such that
| 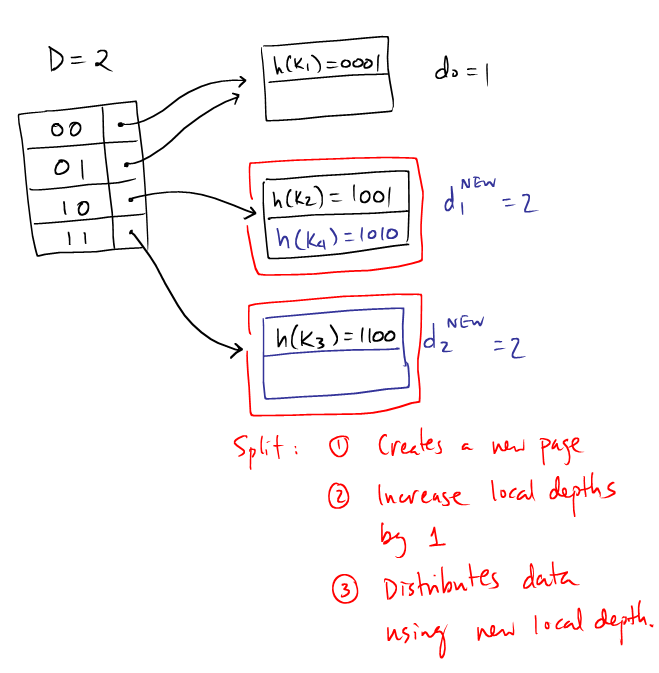 |
| This is the final extended hash table. | 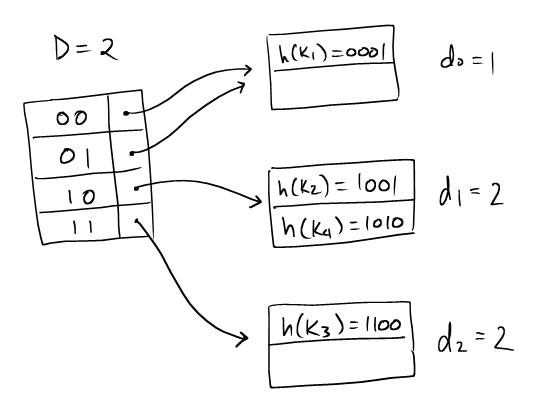 |