B+ tree index
CSC 443
1. Overview of B+ tree
In the previous article, we discussed several important things about indexing:
-
Indexes are disk based data structures to speed up record search (and / or scan)
-
Organizing page pointers into sorted index tree structures speeds up record search. (ISAM)
-
Maintaining sortedness of the index tree is expensive, so we may create overflow pages in ISAM, but the overflow pages degrade search performance from
$\log$ to linear scan.
We will introduce a highly robust and popular data structure B+ tree, which is an extension of ISAM.
Generally speaking, a B+ tree is an efficient disk based data structure that stores (key / value) pairs. It supports very efficient lookup by key, and iteration of entries in the range of two specified key values.
B+ tree offers:
- fast record search
- fast record traversal
- maintaining sorted tree structure without overflow pages
The key idea behind B+ tree is that it utilizes balanced sorted tree of page pointers, as opposed to just sorted tree in the case of ISAM.
2. Definition of B+ tree
A B+ tree is a tree whose nodes are pages on disk. We will distinguish the leaf nodes and the interior nodes of a B+ tree.
Since each node is exactly one disk page, in the context of B+ tree, we use the term page and node interchangably.
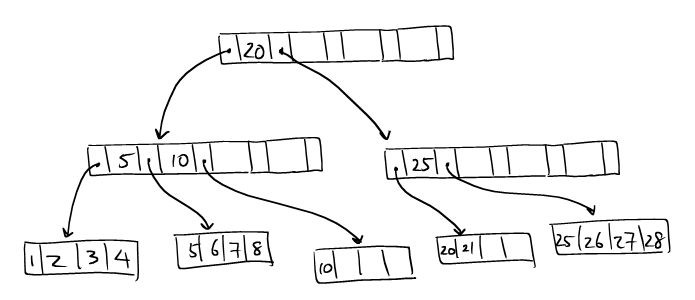
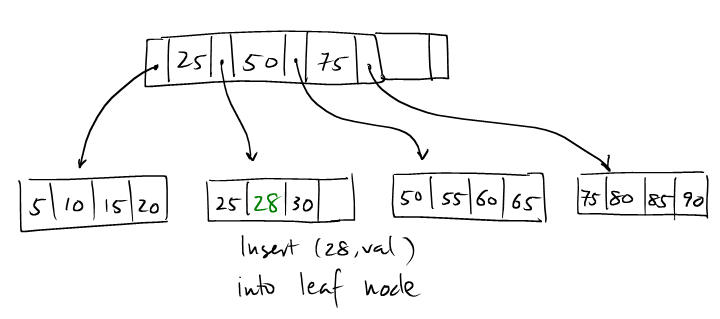
2.1. Leaf nodes
The leaf nodes store the data entries in the form of (key, value). All leaf nodes are also organized into an linked list of pages. Leaf nodes of a B+ tree can be visualized as follows.
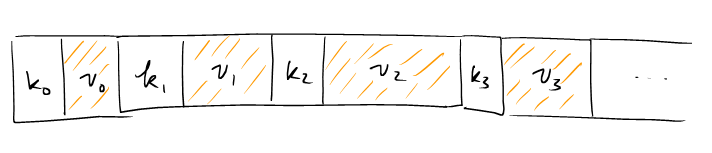
The following data structure abstracts the leaf nodes.
struct LeafNode {
vector<Key> keys;
vector<Value> values;
PagePointer next_page;
}
We can always assert that
p.keys.size() == p.values.size() for all nodes p.
2.2. Interior nodes
The interior nodes form a tree structure, starting from a root node, to speed up lookup of the leaf node that contains a key of interest.
The structure of an interior node can be visualized as a sequence of alternating page pointers and keys.
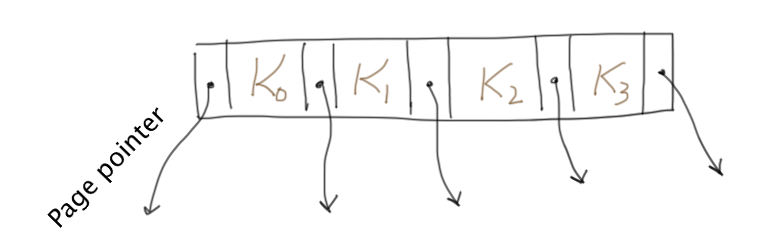
The following data structure abstracts the interior nodes:
struct InteriorNode {
vector<Key> keys;
vector<PagePointer> pointers;
}
We can always assert that p.keys.size() +1 == p.pointers.size().
Definition: Neighbouring pointers
Give a key
Namely,
p.before($k_i$) = p.pointers[i]p.after($k_i$) = p.pointers[i+1]
2.3. Constraints and properties of B+ tree
Keys are sorted in the nodes.
Let p be a node in B+ tree. We need to maintain that
p.keys is sorted by the key values.
Nodes are sorted by their keys
B+ tree is a sorted tree in the following sense:
-
Leaf nodes are sorted:
$$ \forall p\in\mathrm{LeafNode},\; \forall k\in p.\mathrm{keys},\; \forall k'\in p.\mathtt{next\_page.keys},\; k \lt k' $$ The sorted linked list of leaf nodes allows very efficient traveral of (key, value) pairs between two leaf nodes.
-
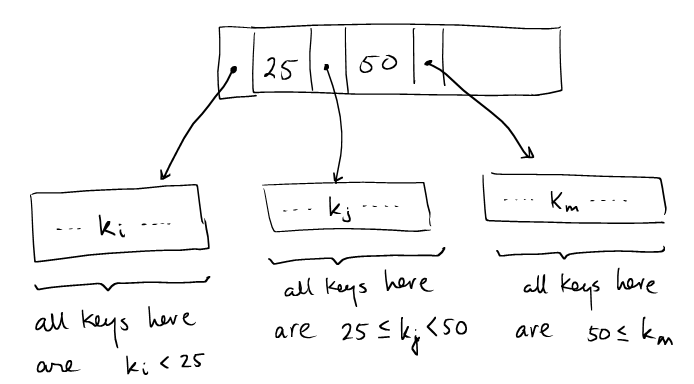
Interior nodes are sorted:
B+ tree asserts that for all key
$k$ and the adjacent pointers,$\mathrm{after}(k)$ and$\mathrm{after}(k)$ , it must be that:$k \gt \max(\mathrm{keys}(\mathrm{before}(k))) $ $k \leq \min(\mathrm{keys}(\mathrm{after}(k))) $
In other words,
$k$ is the key that divides the keys in pages$\mathrm{before}(k)$ and$\mathrm{after}(k)$ .
The tree is balanced
B+ tree is a balanced tree, so all paths from the root to the leaf nodes must be of equal length.
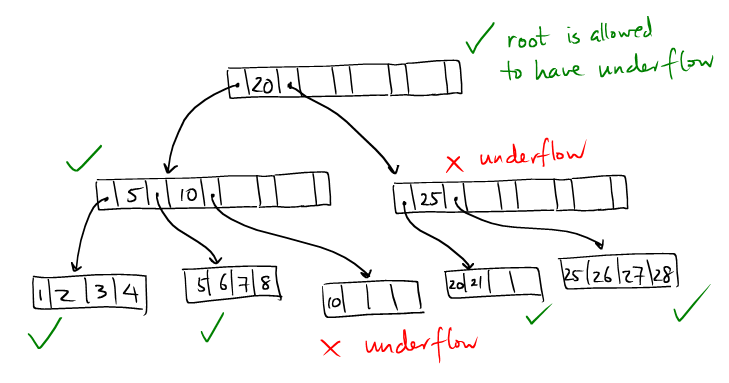
The nodes are sufficiently filled.
B+ tree permits nodes to be partially filled. As a design parameter, B+ tree specifies a percentage, known as the fill factor of the tree, that controls the minimal occupacity of all the non-root nodes.
If a non-root node is too empty, we say it has an underflow. Only the root node can have an underflow.
Here is an example of a problematic B+ tree. Suppose we have the following parameters:
Capacity of each node: 4 keys
Fill factor: 50%
While the tree is balanced and sorted, it does not satisfy the fill-factor.
3. B+ Tree Search and Insertion
The main operations on B+ tree are:
/** * finds the leaf node that _should_ contain the entry with the specified key */ LeafNode search(Node root, Key key) /** * Inserts a key/val pair into the tree. * Returns the root of the new tree which _may_ be different * from the old root node. */ InteriorNode insert_into_tree(InteriorNode root, Key newkey, Value val)
The algorithm for insert must ensure that the
properties of the B+ tree are preserved after the respective operation.
3.1. Searching
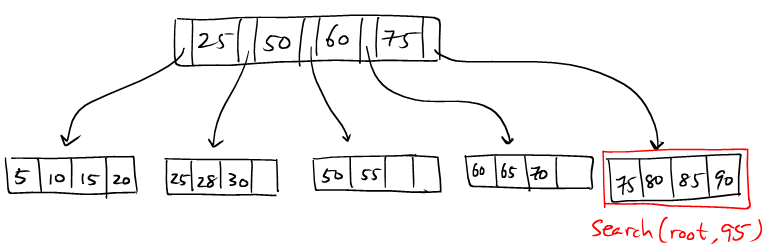
The B+ tree search algorithm is a straight-forward tree traveral algorithm.
LeafNode search(Node p, Key key) {
if(p is LeafNode)
return root;
else {
if(key < p.keys[0])
return search(before(p.keys[0]), key);
else if(key > p.keys[-1])
return search(after(p.keys[-1]), key);
else {
let i be p.keys[i] <= key < p.keys[i+1]
return search(after(p.keys[i]), key)
}
}
}
3.2. Inserting
Insertion into a B+ tree is quite tricky. Unlike the algorithm for insertion into a balanced sorted binary tree, the B+ tree insertion needs to deal with node overflows and underflows.
The insertion algorithm starts with:
- look for the right leaf for insertion
- try to insert into the leaf node
InteriorNode insert_into_tree(InteriorNode root, Key newkey, Value val) {
LeafNode leaf = search(root, newkey);
return insert_into_node(leaf, newkey, val);
}
The insertion algorithm, insert_into_node, looks something like this:
/**
* Tries to inserts the (newkey/val) pair into
* the node.
*
* If `target` is an interior node, then `val` must be a page pointer.
*/
InteriorNode insert_into_node(Node target, newkey, val)
{
if( ... CASE 1 ... ) {
/* handle CASE 1 */
} else if( ... CASE 2 ... ) {
/* handle CASE 2 */
} else if( ... CASE 3 ... ) {
/* handle CASE 2 */
}
}
The tree distinct cases are:
- the target node has available space for one more key.
- the target node is full, but its parent has space for one more key.
- the target node and its parent are both full.
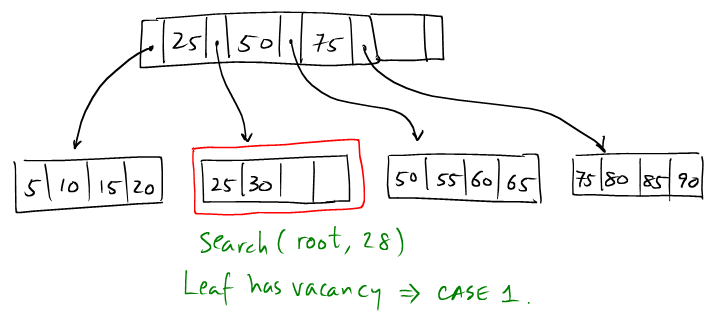
3.2.1. Case 1
This is the easiest case. Simply insert the entry (newkey, val)
into target.
- The root of the B+ tree does not change.
- We have not discussed the disk I/O operations involved. Since all the node operations operate on one page at a time, the buffer manager can be used to provide the transparent virtual memory, as if all the nodes are stored in memory.
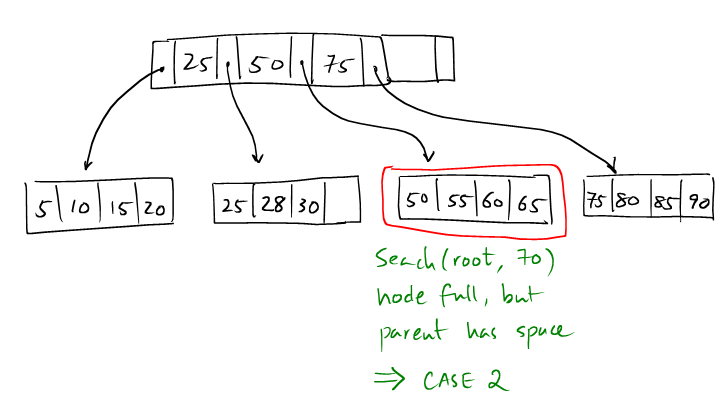
3.2.2. Case 2
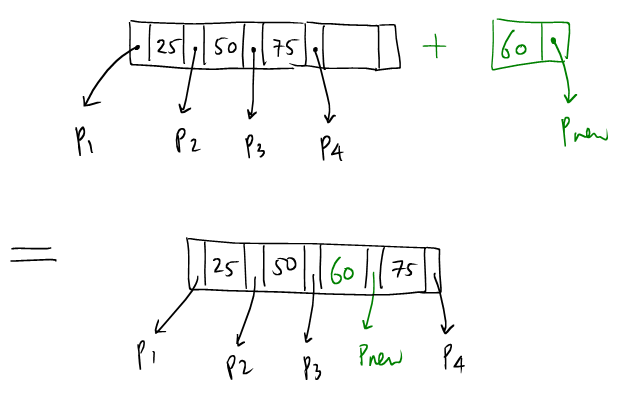
In this case, the target node is full, but its parent node has available space for at least one more key.
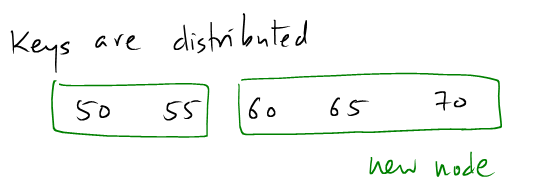
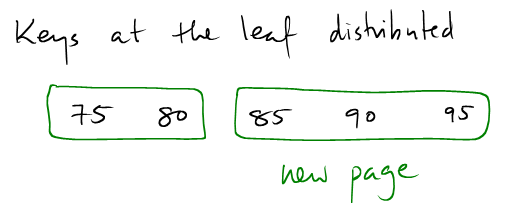
- Create a new sibling node to target, call it
new_target, and insert it aftertarget. - Distribute the data entries between
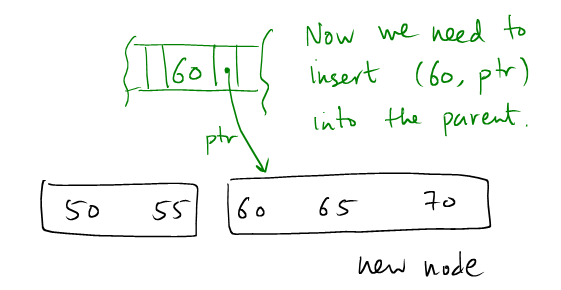
targetandnew_target. From the assumption thattargetis full, we can safely assert that after distribution, there will be no underflow. new_targetmust be pointed to by(k,p) = (leaf2.keys[0], ADDRESS[leaf2])inPARENT[target]. So(k,p)are to be inserted intoPARENT[leaf]. By assumption, we know thatPARENT[leaf]will not overflow.
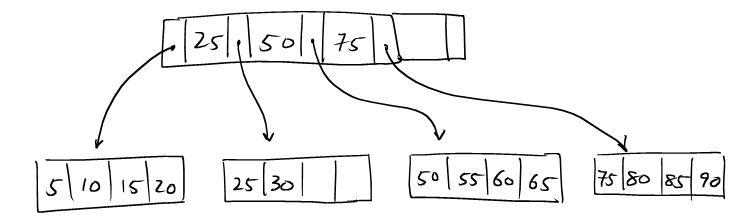
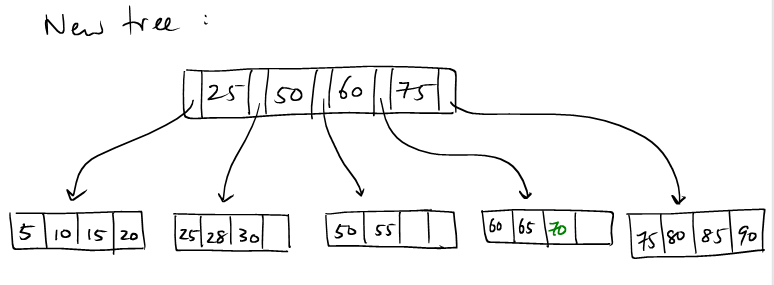
Let's continue with the previous example, and try to insert (70, val).
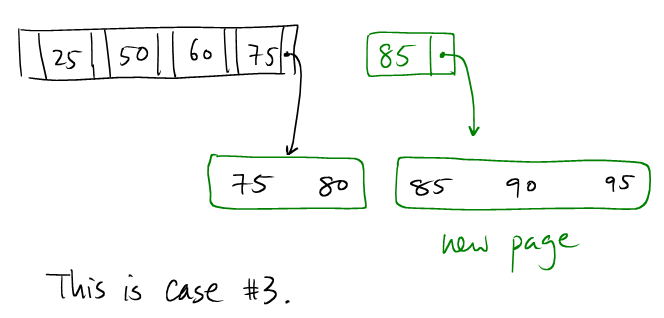
3.2.3. Case 3
This is the case that both target and PARENT[target] are full.
We have to recursively attempt to insert the new key into the
ancestors of target. It is possible that even the root does not have
sufficient space for the new key, in which case we must split the
root, and create a new root node of the B+ tree.
The details are as follows:
- Create
new_targetnode, and insert it aftertarget. - Distribute data entries among
targetandnew_target.
Now, let k = leaf2.keys[0] and p = ADDRESS[leaf2]. We need to
insert (k,p) into PARENT[leaf], which is full.
- Let
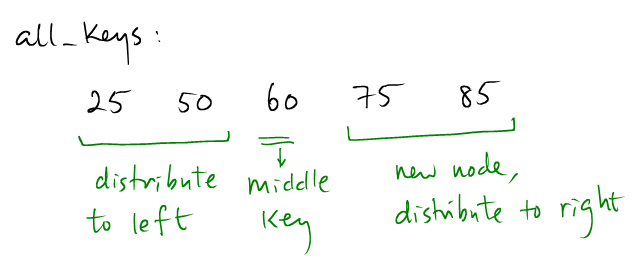
target_parent = PARENT[target] - Let
all_keys = sorted(target_parent.keys $\cup$ {k}) - Allocate new node
new_interior - Let
i = floor(all_keys.size() / 2).
Letmiddle_key = all_keys[i] - Distribute
all_keys[0 .. i-1]totarget_parent, and
Distributeall_keys[i+1 .. n]tonew_interior. - If
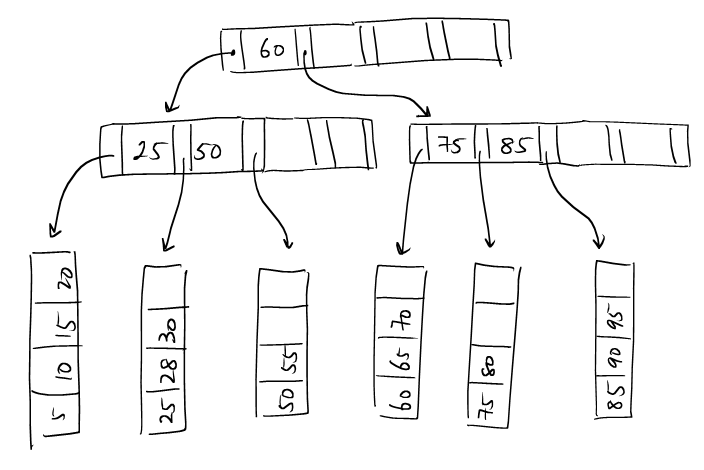
target_parentis the root, then letgrandparentbe a newly allocated node.
Otherwise,grandparent = PARENT[target_parent]. - Recursively call:
insert_into_node(grandparent, middle_key, ADDRESS[new_interior])
4. Other things about B+ Tree
-
B+ tree also offers efficient deletion. The deletion algorithm is a mirror reversal of the insertion algorithm. During deletion, the algorithm trys to merge nodes to avoid underflow. If a merge took place, deletion recursively deletes the
(Key, PagePointer)pair from the parent node. -
If the data entries are stored in a sequential file, sorted by a key, then one can very efficiently bulk load the sequential file into a B+ tree.
-
B+ tree can be used as a sorting algorithm for disk based sorting.