Basic index structures
CSC 443
1. Motivation for indexing
Heap file supports sequential scan of records. Theoretically, this is sufficient to implement all query operators in SQL. However, the resulting efficiency would be impractically poor.
In this article, we discuss a number of simple techniques to improve the efficiency of record scan and record search. The common theme would be:
2. Sequential file
A sequential file is a heap file with the properties:
- all records on a page are sorted by some key attributes,
$K$ .$$ \forall P,\ \forall r_i\in P,\ r_i[K]\leq r_{i+1}[K] $$ - for all pages
$P_i$ and$P_{i+1}$ in the heap file, we have that all records in$P_i$ are less than records in$P_{i+1}$ by the key$K$ .
Thus, a sequential file is with all the records sorted (by key attributes
This one to apply binary search when looking up record(s) by their sorted attribute
Recall the design of the heap file, to look for a record
The total number of disk I/O required in the worst case is:
Sequential file does not address the inefficiency in record scan.
3. Dense indexes
Dense indexes are secondary storage which stores redundant data in order to improve the efficiency of query processing.
Consider the case that a data file already exists.
Let
For each record
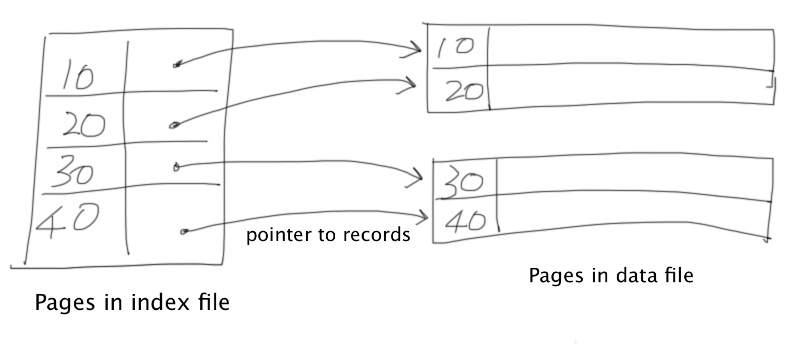
The motivation is that there may be a significant reduction in the record size in the index file when compared to the records in the data file. Thus, each index page contains much more records. Sequential scan through the index file would refer far less disk I/O since there are fewer pages to be retrieved.
4. Sparse indexes
To combine the strengths of sequential files and dense indexes, sparse indexes support binary search for fast record lookup by storing its records sorted by some key
To apply sparse indexes, the data file must be a sequential file, namely data records are sorted by a key
The sparse index only stores the key values and address for the first record of each data page in the data file.
For each data page
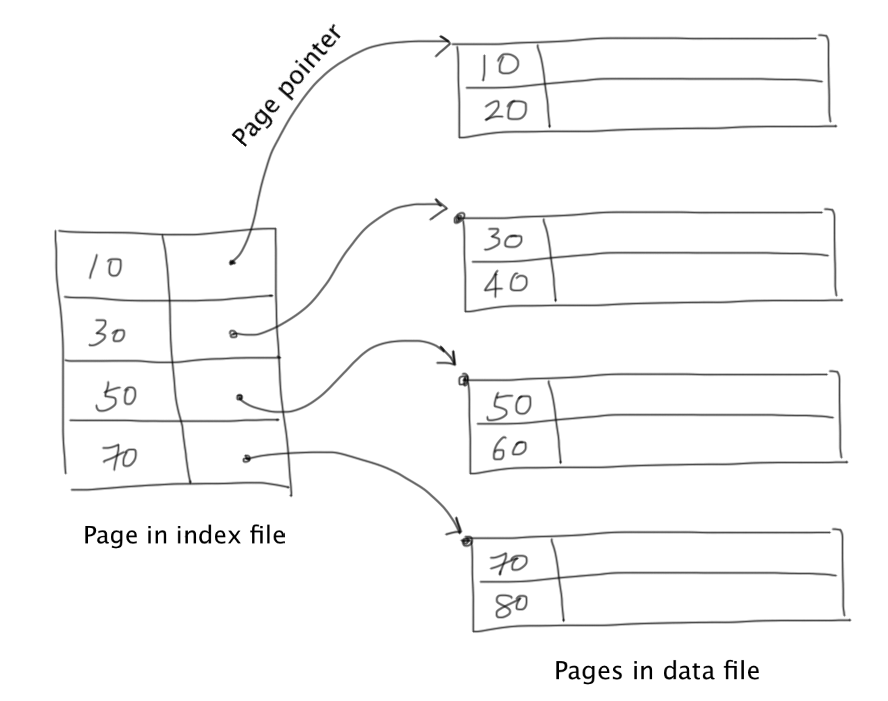
This reduces the number of index pages in the sparse index. Searching for records with
- search in the sparse index for the record
$r$ such that:$$r^* = \mathrm{argmax}_r r[K]\leq \vec{v}$$ Binary search can be used. - search in the page pointed by
$r^*$ for$\{r: r[K] = \vec{v}\}$ .
Assumption: for simplicity, we assume that we only need to retrieve the first occurance of a record
5. Multilevel sparse indexes: tree indexes
Sparse indexes require the data file to be sorted (i.e. a sequential file), and supports record search with:
$\log_2(N_\mathrm{index\ pages})$ page reads are needed to locate the index page.- 1 page read to load the data page.
It turns out that we can improve search even more by making the observation that the sparse index file is a sequential file. So, itself can be indexes by yet another sparse index.
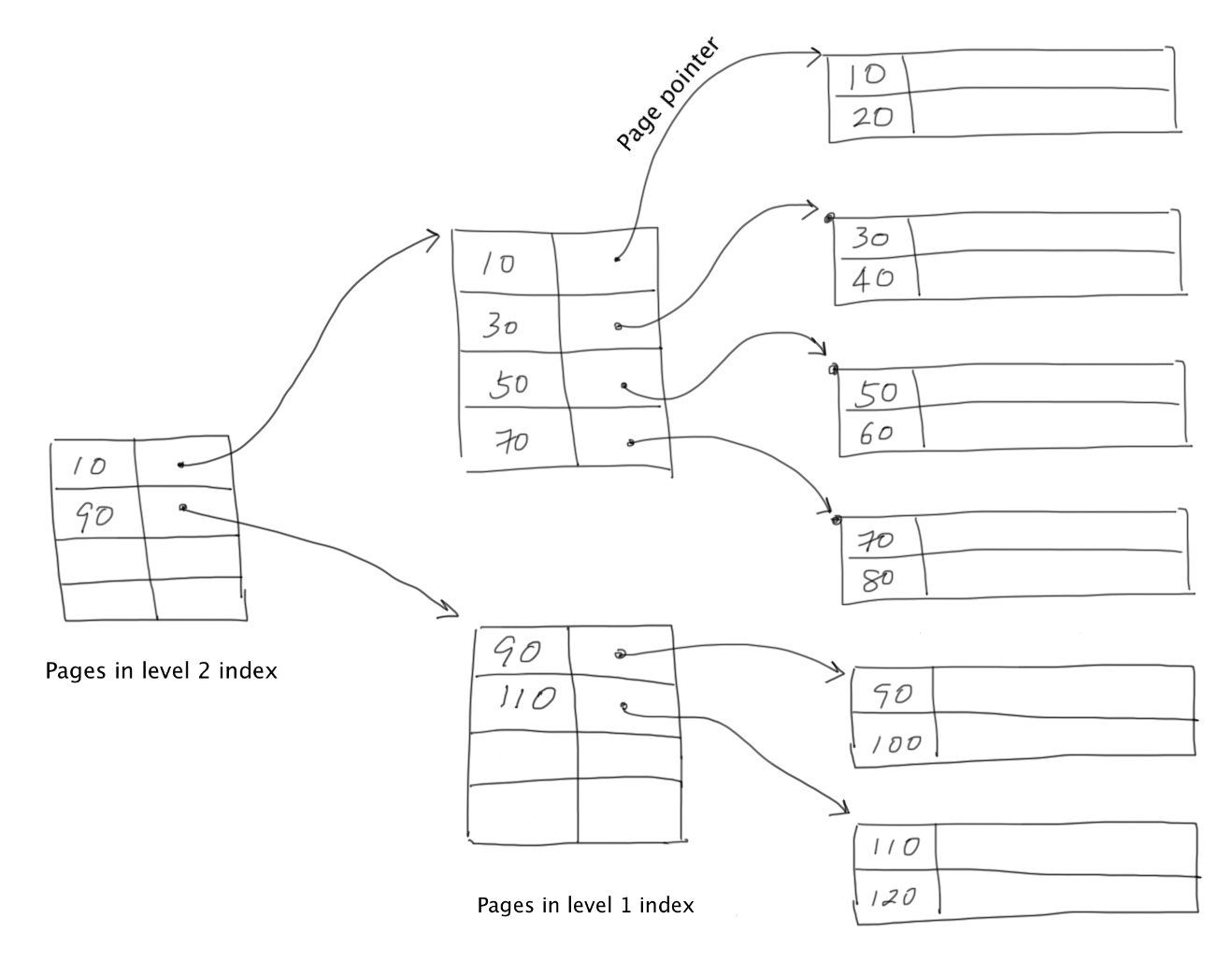
Let
It is the case that:
The number of disk I/Os required for record search is:
$\log_2(N_{I2})$ page reads are used to locate index page in$I_2$ .- 1 page read to load the index page in
$I_1$ - 1 page read to load the data page.
6. Indexed sequential access method (ISAM)
6.1. Limitation of multilevel sparse index
Multilevel sparse index can be applied successively. The number of index pages is reduced at each level, until at the top level, there should be only one index page.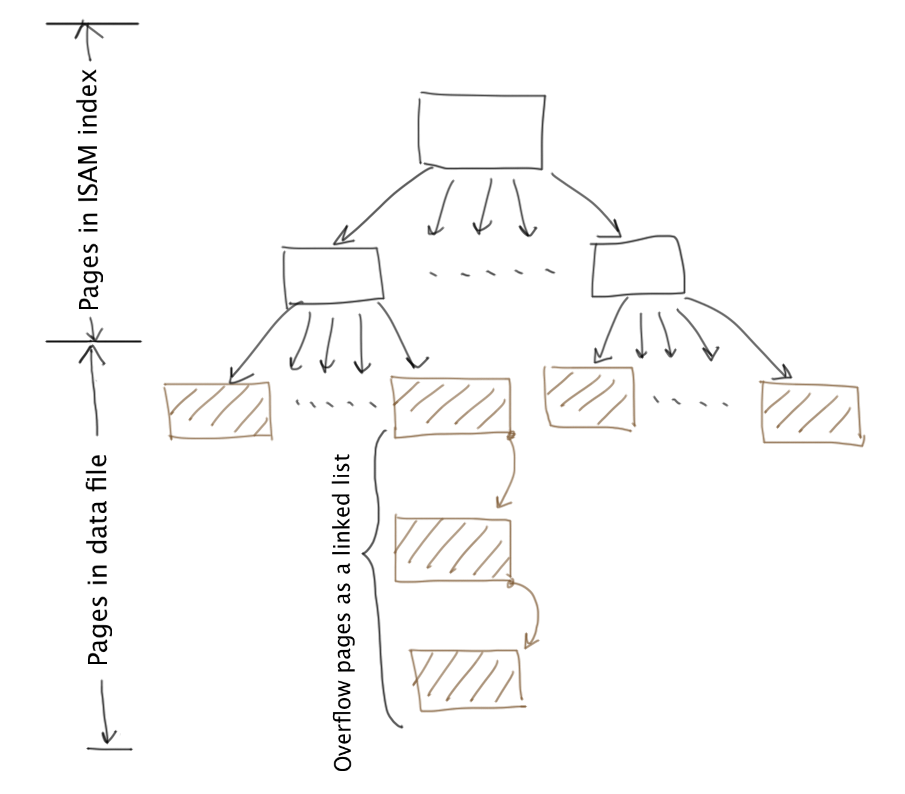
6.2. ISAM
Indexed Sequential Access Method (ISAM) is an indexing technique based on multilevel sparse index, but it overcomes the limitation of multilevel sparse index, and supports fast record insert and update.
The modification is that each data page in the data file can have any number of overflow pages. When inserting a record
- locate data page
$P_i$ such that$P_i[0][K]\leq r[K] < P_{i+1}[0][K]$ . - if
$P_i$ has free space, insert$r$ into$P_i$ . - if there is an overflow page,
$Q$ , of$P_i$ that has free space, insert$r$ into$Q$ . - if all the overflow pages are also full, create a new overflow page to store
$r$ .
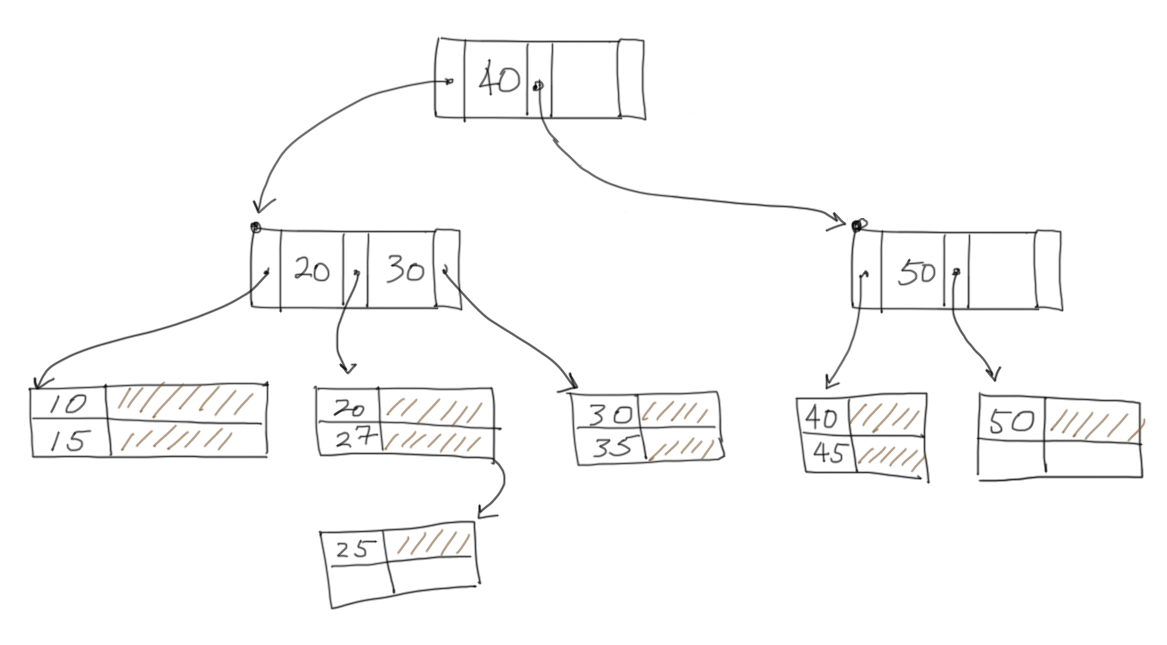
Note: The record (25, ...) is inserted after the index is built. Since there is no space available in the page(s) between the key 20 and 30, ISAM must create a new page which is appended into the appropriate linked list. The insertion of (25, ...) creates an overflow page.
6.3. Limitation of ISAM
ISAM relaxes on the sortedness of records. Consequently, the worst case performance for record retrieval becomes
The cause of the limitation of ISAM is that the multilevel sparse indexes are static in the presence of data updates.
We will discuss the index structure, B+ tree, which addresses the performance degradation of ISAM by means of dynamic tree balancing.