18.2 Selection Sort

We’ll begin our study of sorting in earnest with two different iterative, or loop-based, sorting algorithms. In this section we’ll study selection sort, and in the following section we’ll study insertion sort. Even though these two algorithms solve the same problem (take a list and sort it), they use different approaches that we will be able to compare and learn from.

The algorithm idea

The selection sort algorithm has at its core a fairly intuitive idea. Given a collection of unsorted elements, we repeatedly extract the smallest element from the collection, building up a sorted list from these elements. Selection sort gets its name from the fact that at each step, we select the smallest element from the ones remaining.

For example, suppose we start with the list [3, 7, 2, 5].

• The smallest element is 2, so that becomes the first element of our sorted list: [2].
• The remaining elements are [3, 7, 5]. The smallest element remaining is 3, and so that is the next element of our sorted list: [2, 3].
• The remaining elements are [7, 5]. The smallest element remaining is 5, and our sorted list becomes [2, 3, 5].
• The remaining element is [7]. The smallest element is 7, and our sorted list becomes [2, 3, 5, 7].

We can summarize this behaviour in the table below:

This table looks an awful lot like a loop accumulation table, and indeed we can implement this version of selection sort using a loop.

def selection_sort_simple(lst: list) -> list:
    """Return a sorted version of lst."""
    sorted_so_far = []

    while lst != []:
        smallest = min(lst)
        lst.remove(smallest)
        sorted_so_far.append(smallest)

    return sorted_so_far

This implementation does correctly return a list, but has a significant flaw: it mutates its input lst, which is not documented in its specification. For example, the built-in sorted function also returns a new list, but it makes sure not to mutate its input. We could fix this by, for example, making a copy of lst and operating on that copy instead. However, for the rest of this section we’ll introduce a new implementation of selection sort that instead mutates its argument, without creating any additional lists.

In-place selection sort

We say that a sorting algorithm is in-place when it sorts a list by mutating its input list, and without using any additional list objects (e.g., by creating a copy of the list). In-place algorithms may still use new computer memory to store primitive values like integers, this additional amount of memory is constant with respect to the size of the input list. We can say that the amount of additional memory used is \(\Theta(1)\), ignoring the amount of memory used to store the input itself.

So to implement an in-place version of selection sort, we cannot use a new list to accumulate the sorted values. Instead, our approach will move elements around in the input list, so that at iteration i in our loop, the first i elements of the list are the sorted part, and the remaining parts are unsorted.

Here is our above example of sorting the list [3, 7, 2, 5], now using this in-place approach.

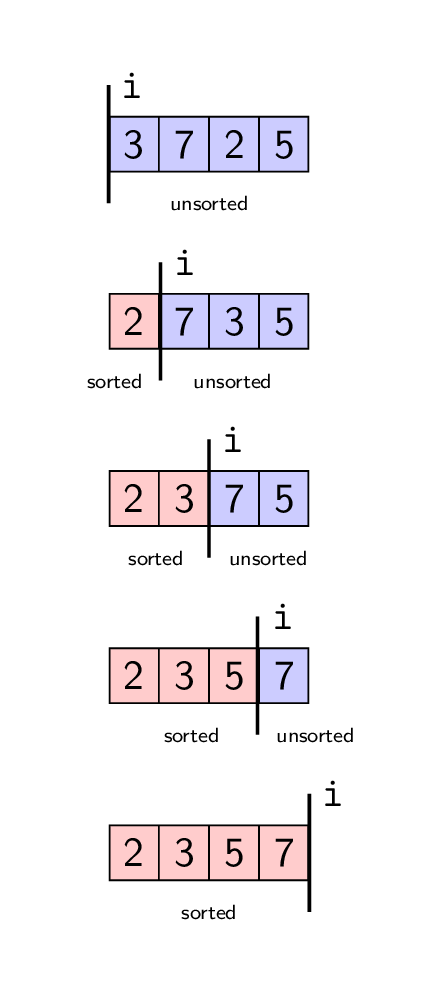
So in this example, i starts at 0.

1. At iteration i = 0, the entire list is unsorted. We find the smallest element in the list (the 2), and swap it with the item at index 0, obtaining the list [2, 7, 3, 5].
2. Then at iteration i = 1, only the elements [7, 3, 5] are unsorted. We again do a swap, moving the 3 to index 1, obtaining the list [2, 3, 7, 5].
3. This repeats again for i = 2, and the 7 and 5 get swapped, so that we get [2, 3, 5, 7].
4. When i = 3, the “unsorted” part consists of just a single number, and so no more swaps occur. The list is sorted!

Some loop invariants

In the above diagram, we used the variable i to represent the boundary between the sorted and unsorted parts of the list. We can represent this formally as a loop invariant. Here is a partial implementation of this in-place selection sort algorithm, with this loop invariant:

def selection_sort(lst: list) -> None:
    """Sort the given list using the selection sort algorithm.

    Note that this is a *mutating* function.
    """
    for i in range(0, len(lst)):
        assert is_sorted(lst[:i])

        ...


def is_sorted(lst: list) -> bool:
    """Return whether this list is sorted."""
    # Implementation omitted

There is another loop invariant that is useful for our implementation of selection sort. At iteration \(i\), the first \(i\) items aren’t just sorted; because we’ve always chosen the smallest item at each iteration, the first \(i\) items must be smaller than all other items in the list. We can express this as a second loop invariant:

def selection_sort(lst: list) -> None:
    """Sort the given list using the selection sort algorithm.

    Note that this is a *mutating* function.
    """
    for i in range(0, len(lst)):
        assert is_sorted(lst[:i])
        assert i == 0 or all(lst[i - 1] <= lst[j] for j in range(i, len(lst)))

        ...

Implementing the loop

Now that we have our loop invariants in place, let’s get to implementing the loop. Remember that at iteration i, we need to find the smallest item in the “unsorted” section of the list, which is lst[i:], and swap it with lst[i].

Here is our full implementation of this function. We’ve pulled out the code to find the smallest item in the unsorted portion into a helper.

def selection_sort(lst: list) -> None:
    """Sort the given list using the selection sort algorithm.

    Note that this is a *mutating* function.

    >>> lst = [3, 7, 2, 5]
    >>> selection_sort(lst)
    >>> lst
    [2, 3, 5, 7]
    """
    for i in range(0, len(lst)):
        # Loop invariants
        assert is_sorted(lst[:i])
        assert i == 0 or all(lst[i - 1] <= lst[j] for j in range(i, len(lst)))

        # Find the index of the smallest item in lst[i:] and swap that
        # item with the item at index i.
        index_of_smallest = _min_index(lst, i)
        lst[index_of_smallest], lst[i] = lst[i], lst[index_of_smallest]


def _min_index(lst: list, i: int) -> int:
    """Return the index of the smallest item in lst[i:].

    In the case of ties, return the smaller index (i.e., the index that appears first).

    Preconditions:
        - 0 <= i <= len(lst) - 1
    """
    index_of_smallest_so_far = i

    for j in range(i + 1, len(lst)):
        if lst[j] < lst[index_of_smallest_so_far]:
            index_of_smallest_so_far = j

    return index_of_smallest_so_far

Running-time analysis for selection sort

To wrap up, let’s analyze the running time of our in-place selection sort algorithm, ignoring the assert statements. We need to first analyze the helper function _min_index. Let \(n\) be the length of the input list lst.

• The statements outside of the loop take constant time. We’ll treat them as just a single step.
• The loop iterates \(n - i - 1\) times, for \(j = i + 1, \dots, n - 1\), and the body takes constant time (1 step). So the running time of the loop is \(n - i - 1\) steps.
• So the total running time of _min_index is \((n - i - 1) + 1\), which is \(\Theta(n - i)\).

Now let’s look at selection_sort. Once again, let \(n\) be the length of the input list lst.

Inside the body of the loop, there are two statements (ignoring the assertions). The first statement is the call to _min_index, which takes \(n - i\) steps, where \(i\) is the value of the for loop variable. Note that we’ve translated the \(\Theta(n - i)\) running time for _min_index into an exact \(n - i\) number of steps in the loop body. The second statement (swapping the lst values) takes constant time, so we’ll count that as 1 step. So the running time of one iteration of the for loop is \(n - i + 1\), and the for loop iterations once for each \(i\) between 0 and \(n - 1\), inclusive.

This gives us a total running time of:

\[\begin{align*} \sum_{i=0}^{n - 1} n - i + 1 &= n(n + 1) - \sum_{i=0}^{n - 1} i \\ &= n(n + 1) - \frac{n(n - 1)}{2} \\ &= \frac{n(n + 3)}{2} \end{align*}\]

Therefore the running time of selection_sort is \(\Theta(n^2)\).

References

• CSC108 videos: Selection Sort (Part 1, Part 2)