\( \newcommand{\NOT}{\neg} \newcommand{\AND}{\wedge} \newcommand{\OR}{\vee} \newcommand{\XOR}{\oplus} \newcommand{\IMP}{\Rightarrow} \newcommand{\IFF}{\Leftrightarrow} \newcommand{\TRUE}{\text{True}\xspace} \newcommand{\FALSE}{\text{False}\xspace} \newcommand{\IN}{\,{\in}\,} \newcommand{\NOTIN}{\,{\notin}\,} \newcommand{\TO}{\rightarrow} \newcommand{\DIV}{\mid} \newcommand{\NDIV}{\nmid} \newcommand{\MOD}[1]{\pmod{#1}} \newcommand{\MODS}[1]{\ (\text{mod}\ #1)} \newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\C}{\mathbb C} \newcommand{\cA}{\mathcal A} \newcommand{\cB}{\mathcal B} \newcommand{\cC}{\mathcal C} \newcommand{\cD}{\mathcal D} \newcommand{\cE}{\mathcal E} \newcommand{\cF}{\mathcal F} \newcommand{\cG}{\mathcal G} \newcommand{\cH}{\mathcal H} \newcommand{\cI}{\mathcal I} \newcommand{\cJ}{\mathcal J} \newcommand{\cL}{\mathcal L} \newcommand{\cK}{\mathcal K} \newcommand{\cN}{\mathcal N} \newcommand{\cO}{\mathcal O} \newcommand{\cP}{\mathcal P} \newcommand{\cQ}{\mathcal Q} \newcommand{\cS}{\mathcal S} \newcommand{\cT}{\mathcal T} \newcommand{\cV}{\mathcal V} \newcommand{\cW}{\mathcal W} \newcommand{\cZ}{\mathcal Z} \newcommand{\emp}{\emptyset} \newcommand{\bs}{\backslash} \newcommand{\floor}[1]{\left \lfloor #1 \right \rfloor} \newcommand{\ceil}[1]{\left \lceil #1 \right \rceil} \newcommand{\abs}[1]{\left | #1 \right |} \newcommand{\xspace}{} \newcommand{\proofheader}[1]{\underline{\textbf{#1}}} \)

1.6 Storing Data in Variables

So far, we’ve been writing expressions in the Python console using only literals and operators. But as the computations we want to perform get more complex, relying on just literals and operators is very cumbersome. We can write very complex nested expressions, but this makes our code very hard to understand.

For example, suppose we’re given three points in the Cartesian plane \((1, 3)\), \((2, 5)\), \((10, -1)\) that form a path, and we want to find the length of this path.

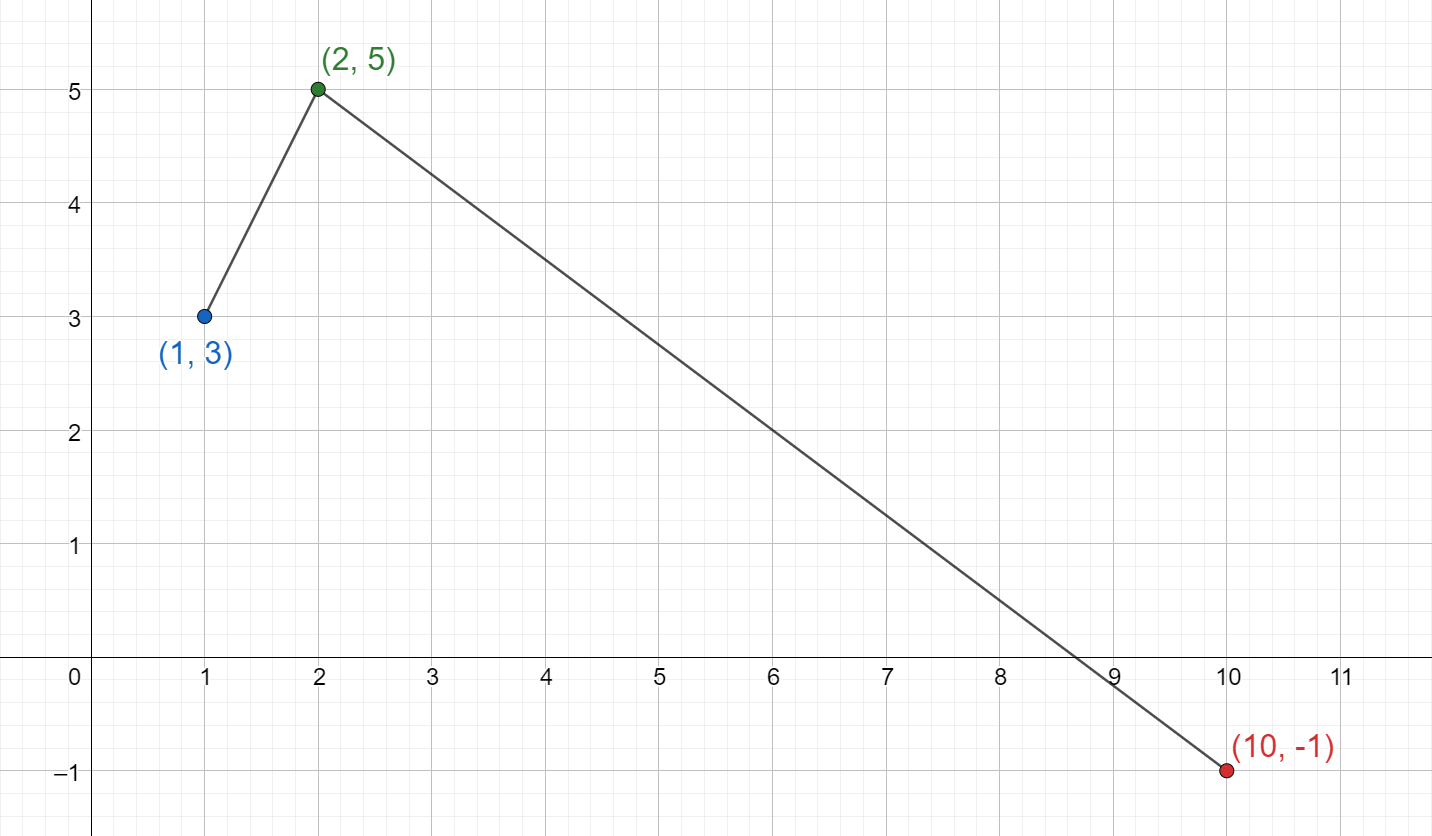
A diagram of the Cartesian plane showing a path connecting points (1, 3), (2, 5), and (10, -1)

We’d like to use this formula for the distance \(d\) between two points \((x_1, y_1)\) and \((x_2, y_2)\):

\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}. \]

We could write the path length calculation as a single arithmetic expression and have Python evaluate it:

>>> ((2 - 1) ** 2 + (5 - 3) ** 2) ** 0.5 + ((10 - 2) ** 2 + ((-1) - 5) ** 2) ** 0.5
12.23606797749979

But typing this expression is quite error-prone and hard to understand. Just like in mathematics, we can improve our code by breaking down this problem into intermediate steps. In Python, we can do so by associating values to names, so that we can refer to those values later on in subsequent calculations.

Variables

A variable is a piece of code consisting of a name that refers to a value. We create variables in Python using the syntax:

<variable> = <expression>

which is a form of Python code called an assignment statement. You might wonder why we use the term “statement” rather than “expression” for assignment. An expression is a piece of Python code that is evaluated to produce a value. When we execute an assignment statement, the code doesn’t produce a value—it instead defines a variable and assigns a value to that variable.

Python executes an assignment statement in two steps:

  1. First, the expression on the right-hand side of the = is evaluated, producing a value.
  2. Second, that value is bound to (or “assigned to”) the variable on the left-hand side.

After the assignment statement is executed, the variable may be used to refer to the value. Here’s how we can use variables to simplify the calculation above:

>>> distance1 = ((2 - 1) ** 2 + (5 - 3) ** 2) ** 0.5   # Distance between (1, 3) and (2, 5)
>>> distance2 = ((10 - 2) ** 2 + ((-1) - 5) ** 2) ** 0.5  # Distance between (2, 5) and (10, -1)
>>> distance1  # A variable is an expression; evaluating it produces the value it refers to
2.23606797749979
>>> distance2
10.0
>>> distance1 + distance2  # The total distance
12.23606797749979

Choosing good variable names

Because variables are used to store intermediate values in computations, it is important to choose good variable names so that you can remember what the purpose of each variable is. This might not seem that important in our above example because there were only two variables, but as you start writing larger programs, you’ll have to grapple with dozens, if not hundreds, of variables, and choosing good names will be paramount.

For now, we’ll introduce a few simple rules that you should follow when choosing variable names:

  1. All variable names should use only lowercase letters, digits, and the underscore character. So distance1, not Distance1.

  2. When a variable name consists of multiple words, separate each word with an underscore. You aren’t allowed to use spaces in variable names, so underscores are used to show word breaks instead. For example, we might create a variable to refer to the total distance by writing

    >>> total_distance = distance1 + distance2

    We use the variable name total_distance rather than totaldistance or totalDistance.Variable naming conventions vary across programming languages. For example, totalDistance would be the standard choice for this variable name when using the Java programming language.

  3. Avoid single-letter variable names and non-standard acronyms/abbreviations, outside of some mathematical contexts.

    For example, we might have used d1 and d2 instead of distance1 and distance2 because d is the variable we used for distance in our above formula. However, we should not use td instead of total_distance, because a new person wouldn’t immediately understand what td stands for.

The value-based Python memory model

As our programs get larger, it is useful to have a way to keep track of the variables and data used. A memory model is a structured representation of variables and data in a program. The term “memory” here refers to the computer memory used to actually store the data. For the next few weeks, we’re going to use the value-based Python memory model, which simply uses a table to represent the association between each variable and their associated value. For example, the value-based memory model for our above example is the following:

Variable Value
distance1 2.23606797749979
distance2 10.0
total_distance 12.23606797749979

References