Knapsack problem
You have a knapsack (backpack). You come across a room out of a Tolkien story: filled with gold and silver coins, and all sorts of things.You can carry a certain volume, or perhaps weight, of coins. Your knapsack has some capacity, in some sort of units. You have to walk ten kilometres home so you're not going to carry anything any other way than in your knapsack.
Is it best to fill it up with gold coins or silver coins? Gold coins are worth more, but they are heavier.
Gold coins, though, are worth more money per gram. So if you can carry a set amount of weight, you would prefer gold coins. It depends on how they're made, so let's say that the gold coins in this room are worth less money per millilitre (or per litre) than the silver coins. So if you have a capacity of a certain amount of space, you would prefer the silver coins.
In any case, if you stuff your knapsack with all the coins you can of the one which gives you the most value for the cost, you may end up with some space or weight allowance left over.
You may take all the gold coins in the room, for example, and then have to start on the silver coins (unless you want to waste some of the room in your knapsack).
Or you may fill your knapsack until it has no room for any more gold coins, but isn't quite full; perhaps there's space left which is equivalent to space for 0.8 gold coins. If there are some other coins which are smaller or lighter, you may be able to fit a few of those.
Perhaps if you leave out one gold coin, that 1.8 gold coins' worth of space can carry enough silver coins such that their value is greater than 1 gold coin, even though we know it's less than 1.8 gold coins.
So there are many considerations involved, and it's not trivial to write a computer program to solve it other than by "brute force", trying all possibilities. That algorithm ends up taking exponential time, so we'd like to do better.
Another example of a related situation is packing a box for moving. The box has a certain volume; or you may have a maximum weight for the box. So you might fill it up with large objects, and then squeeze some smaller objects in there too.
Here is a precise and formal definition of the knapsack problem. Not everything in the examples above applies to the knapsack problem. In particular, we assume we can't run out of a particular kind of item.
Knapsack problem:
Given a non-negative integer capacity C, non-negative integer "weights" (costs) w0, w1, ..., wn-1 of n different kinds of items, and their integer values (utility) v0, v1, ..., vn-1:
Find the list of indices I0, I1, ..., Ik-1 (repetitions allowed)
such that 
and 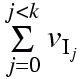 is maximal.
is maximal.
Working on a knapsack problem solution:
It's hard even to see how to write the "brute-force" solution. We have to enumerate all candidate solutions, but there's an infinite number, because we can have any number of each item.
Actually we can fill the knapsack with only one kind of item at a time, and thus make a list of the maximum possible numbers of each individual item. This will be a lot of combinations, but it yields the brute-force approach.
The time complexity of the resulting algorithm will be something like the number of kinds of items to the power of the capacity. That is, this is an exponential-time algorithm, which is generally considered unacceptable.
To come up with a recursive or dynamic-programming solution, we need to figure out what kinds of partial solutions are of interest. That is, we need the formula for the reduced parameter in the recursive call.
Subproblems with fewer items or smaller weights don't end up yielding an interesting recursion.
The only thing which leads to a useful sub-problem is smaller capacities.
But it's tricky. If we have an optimal selection of objects for a capacity of ten, and another optimal selection of objects for a capacity of 15, if we combine those two groups we don't necessarily have an optimal selection of objects for a capacity of 25. We have a possible selection of objects for a capacity of 25, but not necessarily the best. For example, there could be an object of great value but a cost of 20, which we couldn't consider in the 10 or 15 cases, but is now an option.
However, this does work the other way around! If we have an optimal solution for cost 25, and if it contains some items which have a total cost of 10, then if we remove those items, we necessarily have an optimal solution for size 15.
This is not a contradiction because in the case of that valuable item of size 20, the sub-problem under consideration differs! That is, some set of subproblems (in terms of reduced capacity) do constitute a partial solution to the big problem, and some don't.
This consideration of subproblems yields a recurrence. The basis of recursion, or of dynamic programming, is a recurrence. We want to separate the recurrence from our choice of implementation, whether it's recursion, memoization, or dynamic programming, or what.
So we work on the recurrence first:
Let M(j) = maximum value attainable for capacity j
(Knapsack problem solution is M(C))
Recurrence:
M(0) = 0
For j>0, M(j) = max(
M(j-1),
MAX i such that wi <= j of M(j-wi) + vi)
Here "MAX" is a quantifier and "max" is a two-argument function.
The above recurrence says that the maximum value attainable for capacity j is the maximum of
- the maximum value attainable for capacity j-1 (this represents leaving some empty space, but sometimes that's best)
- for each kind of item 'i', the maximum value attainable for (j-weight[i]), plus the value of an item of type i. This represents taking out one item of type i from the container of capacity j, finding an optimal sub-solution, then putting that item of type i back in to find the optimal solution for j.
Recursive function:
int M(int j)
{
int i, max;
if (j == 0)
return 0;
max = M(j-1);
for (i = 0; i < n; i++) {
if (w[i] <= j) {
int subvalue = M(j - w[i]) + v[i];
if (subvalue > max)
max = subvalue;
}
}
return max;
}
This is pretty nasty.
For the same reason as recursive Fibonacci, but worse -- n recursive calls
instead of 2.
So it's
exponential. Not much better than the "brute-force" algorithm.
However, the dynamic-programming algorithm for this recurrence turns out to be pretty good!
Dynamic-programming version:
M[0] = 0;
for (j = 1; j <= C; j++) {
M[j] = M[j-1];
for (i = 0; i < n; i++)
if (w[i] <= j && M[j - w[i]] + v[i] > M[j])
M[j] = M[j - w[i]] + v[i] ;
}
This is nice.
Just about O(n2).
We're not quite done; this doesn't actually give the solution! This finds the maximum value, but it doesn't find the list of indices, the list of "I want a gold coin, a silver coin, another gold coin, another gold coin."
But like what we said about the statistics-tracking in your simulation, the structure of the above program parallels the actual problem well enough that we can in a straightforward way add enough tracking to it to get the actual answer.
We keep another array which for all j, specifies ANY ONE OF the items involved in attaining a value of M[j]. Why is any one good enough? Because we can then look at the subproblem of C minus that item's weight and find another one, and so on.
Thus the solution extraction will be recurrent too.
Let L[i] (for "last") be the last item added in attaining the best allocation for C.
// compute best packing
M[0] = 0;
L[0] = -1; // signal saying there are no more items in the list
for (j = 1; j <= C; j++) {
M[j] = M[j-1];
L[j] = L[j-1];
for (i = 0; i < n; i++) {
if (w[i] <= j && M[j - w[i]] + v[i] > M[j]) {
M[j] = M[j - w[i]] + v[i] ;
L[j] = i;
}
}
}
// extract solution
for (j = C; L[j] >= 0; j -= w[L[j]])
printf("%d\n", L[j]);
Example: C = 11,