The first design idea is similar to the stack (see question #5), except that the output line comes from the oldest-added item in the queue. The trick is that we don't know whether that's item #1 or #2. So to get the output line right, we have to keep track of the current size of the queue, as suggested in the question. Then, an 'add' adds one to this value and moves everything down in the queue, whereas a 'leave' subtracts one from the size value and moves everything up.
This ends up being moderately complicated, and given the maximum queue size of two, there are simpler possible circuits. First of all, note that the four flip-flops involved in a circuit along the preceding design lines yields 2**4 (16) possible system states, whereas there are in fact only seven possible valid states:
So it seems we should only need three flip-flops, because three flip-flops can represent up to eight distinct states. Can we design this sparser circuit?
In fact, we know right away that we can. All we have to do is to make a list of, for each of these seven states and for all input possibilities, which state to go to next. Then we just have a three-bit register containing a number from 0 to 6 (it won't ever be 7, because that would be an eighth state), whose input is an extremely complex combinational circuit which performs this state transition.
The resulting circuit will be pretty wonky, so we won't do that unless we can't find a three-flip-flop answer in a more obvious manner.
In fact there is a further simplification which is possible. We do not, in fact, have to distinguish between one of the size-two states and the empty state, because the set of valid operations is disjoint.
Still, 6 is between 2**2 and 2**3, so we still need three flip-flops. (This could have been a reduction in the number of flip-flops under other circumstances, e.g. if we had a list of 9 states and this manipulation reduced it to 8...)
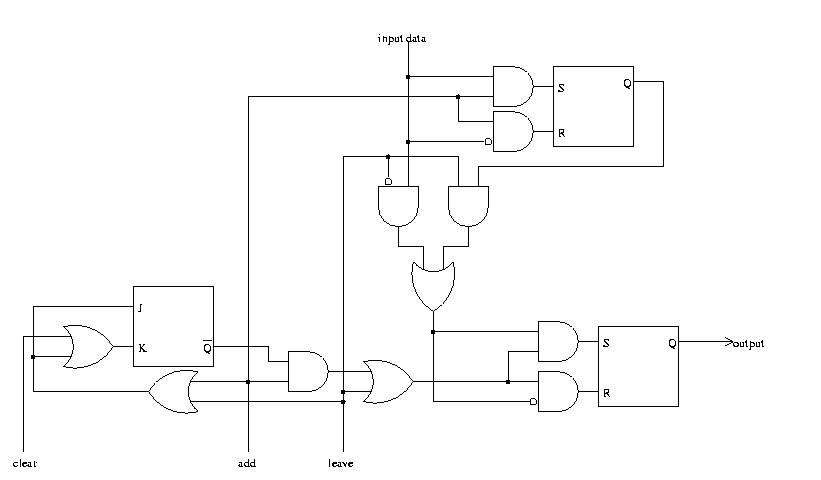
We'll use this observation anyway. In the circuit below, the JK flip-flop in the lower left represents the boolean statement "the size of the queue is 1". We don't need to distinguish between the two states for which this statement is false (sizes 0 and 2). Another way to say it is that this JK flip-flop contains the low bit of the queue size: 0 for 00 and 10, and 1 for 01.
If the size of the queue is 1, we store an "ADD"ed value into the upper-right flip-flop, which represents the item which is second-to-the-head of the queue, i.e. not the first item which will "LEAVE".
If the size of the queue is 0 (or 2, but in the 2 case it is being used incorrectly when we do another ADD and thus this incorrect behaviour is allowed), then we store an "ADD"ed value into the lower-right flip-flop, which represents the item which is at the head of the queue, i.e. the first item which will "LEAVE".
We then observe that we actually don't need to worry about circuitry to suppress the storage of this value into the upper-right flip-flop, too. It won't hurt anything there.
In the case of a LEAVE, we move the data values down. This involves merely copying the data value in the upper-right flip-flop into the lower-right flip-flop. So there are two possible input sources for the lower-right flip-flop: via a LEAVE, and when ADDing a data value to an empty queue. Thus we use our standard anding-the-data-values-with-the-control-functions-and-oring-together-the-results.
Altogether we have the following formulas for the data and control lines for the two SR flip-flops. We implement a control line by ANDing the data with the control line for the S input line, and ANDing the inversion of the data with the control line for the R input line. This is then similar to the D flip-flop design.
Altogether we have the following (you may have to scroll to the right):

The remaining cute thing to observe is about the operation of that JK flip-flop. It is reset (made zero) when there is a CLEAR, obviously. After this, the size of the queue is zero, not one. (As discussed above, the flip-flop should be on iff the size of the queue is one.)
But when there is an ADD or a LEAVE, it toggles. So ADD and LEAVE go into the ORs going into both J and K. Let's rename the JK flip-flop's output to "odd", i.e. "the size of the queue is odd". Then we see that in the case of an ADD, this toggling turns a 0 (not odd) into 1 (yes odd) and a 1 (yes odd) into 2 (not odd). In the case of a LEAVE, this turns a 2 (not odd) into 1 (yes odd) and a 1 (yes odd) into 0 (not odd). This leaves us unable to distinguish between queue sizes of 0 and 2, but as reasoned in the beginning of this web page, we don't need to be able to.