a)
Write down a formula for the boolean value computed.
(no marks for this sub-part; you can simplify as you go if you like)
Answer:
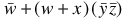
b)
Simplify this to a minimal sum-of-products form formula.
Answer:
=
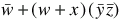
=
 (distribute)
(distribute)
=
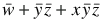 (absorption on w)
(absorption on w)
=
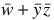 (second absorption law, for a =
(second absorption law, for a = 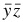 )
)
c)
Your part 'b' answer
is minimal only if "not" operators are considered to be free.
Now suppose that they count as an operator just as much as an AND or an OR.
Produce an equivalent expression which uses fewer
operators, counting the "not" operators.
Answer:
=
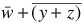
=
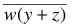 (multiple "extended deMorgan's"es)
(multiple "extended deMorgan's"es)
(one AND, one OR, and one NOT: total of three as opposed to five above)
(yes, this part was hard... more of the marks are for part b.)
[exam]
[CSC 258 additional problems]
[main course page]
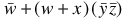
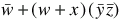
 (distribute)
(distribute)
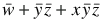 (absorption on w)
(absorption on w)
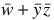 (second absorption law, for a =
(second absorption law, for a = 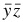 )
)
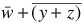
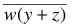 (multiple "extended deMorgan's"es)
(multiple "extended deMorgan's"es)