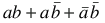
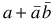=
("no name" law)
=
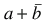(third absorption law)
=
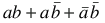
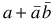("no name" law)
=
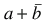(third absorption law)
).
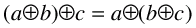Note that
.
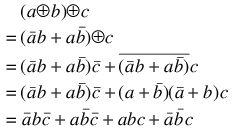
Now, rearrange by commutativity and associativity and go backwards!
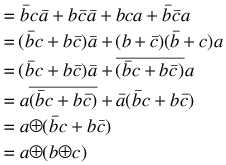
To make a more reasonable answer out of this, you should either have noticed the symmetry between the two halves of the proof (and after that, some ellipsis is allowable!), or else... just use a truth table! We normally eschew truth tables for proofs like these because they're so much longer than an algebraic proof. Not so in this case. A truth table is a very reasonable approach in this case, just because although the truth table is big and cumbersome, the proof is worse.
| a | b | c | (a XOR b) XOR c | a XOR (b XOR c) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
To find a counterexample, note that
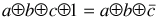
So we want to find 'a' and 'b' ('c' doesn't matter) such that
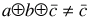
This requires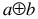 
to be non-zero, e.g. if a=1 and b=0.
So. The counterexample is: Let a=1 and b=c=0.
Then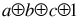 
is 0 and 
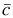is 1,
so it is not always true that .
Whenever 'a' is 1, the left side is going to be 1, and the right side is going to be 1 XOR 1 which is 0, no matter what 'b' and 'c' are.
Many boolean operator pairs distribute, but not OR over XOR.