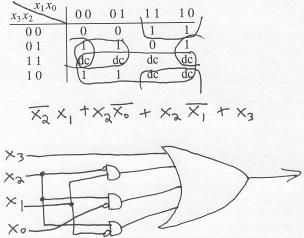
(It is possible to replace the horizontally-wrapping-around group (x2 and not x0 -- the second term in my formula above) with the right-most column of the matrix (x1 and not x0). This merely changes which points are in multiple groups. Since these two groups are both of size four (equivalently, are both expressible with two terms), this is equally "minimal"; the overall functions described are equivalent and this can be shown algebraically.)
1b:
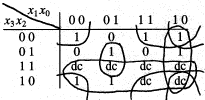
At first, we spend some time fiddling around with columns of numbers and looking for easy patterns -- after all, the question says that we don't have to do the Karnaugh map thing -- but this doesn't yield any easy answers. So we try the Karnaugh map approach anyway:

But that's such an awful Karnaugh map that we see why the exam question suggested that this was not a required approach.
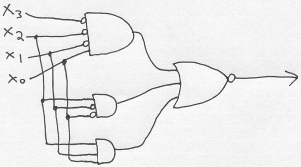
The bottom-middle segment is off for only 1, 4, and 7. So let's draw AND gates representing each of these numbers, and then NOR them together to get an output which says that "the value is not 1, 4, or 7".
The value 1 can be detected by ANDing together not-x3, not-x2, not-x1, and x0. That is, x3, x2, and x1 are off whereas x0 is on.
For the values 4 and 7, we can ignore the state of x3 because if it is on, that is a "don't care" situation.
This yields the following circuit: