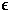CSC 236 midterm, day section

1.
a) Prove that for all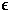 nN, 

Solution:

b) Prove that the following program is partially correct (i.e. you do not need to prove termination).

Precondition: n>=0
Postcondition: x = n² - n + 5
Loop invariant: x = i² - i + 5

x := 5
i := 0
while i < n do
    x := x + i + i
    i := i + 1
end while

Solution:

Let P(i) = (After i loop iterations, where i=0 means at the beginning of the first loop iteration, x = i² - i + 5.)

Base case: P(0) = (before the loop, 5 = 0² - 0 + 5), which is true.

Now assume P(i), for any i, and prove P(i+1), which is that x+i+i = (i+1)² - (i+1) + 5.

By the inductive hypothesis,
x+i+i = (i² - i + 5) + i + i
= i² + 2i - i + 5
= i² + 2i + (1 - 1) - i + 5
= (i² + 2i + 1) - (i+1) + 5
= (i+1)² - (i+1) + 5

2. The Fibonacci numbers can be defined as follows:

F(0) = 0
F(1) = 1
For iZ, where i>=2, F(i) = F(i-1) + F(i-2)

The following program computes the nth Fibonacci number, where all variables are of type int:

i := 1
thisnum := 1
lastnum := 0
while i < n do
    nextnum := thisnum + lastnum
    lastnum := thisnum
    thisnum := nextnum
    i := i + 1
end while

a) Using "F(i)" to indicate the ith Fibonacci number, specify a precondition and a postcondition for this program.

Solution:
Precondition: n>0
Postcondition: thisnum = F(n)

b) Using "F(i)" to indicate the ith Fibonacci number, specify a loop invariant for the `while' loop.

Solution: thisnum = F(i) AND lastnum = F(i-1)

c) We can prove the termination of this program by observing certain crucial facts about the value of n minus i. State any two of them.

Solution: State any two:

• it is an integer
• it is strictly decreasing
• the loop terminates when it is no longer positive (OR: the loop terminates when it hits zero, and it can't miss hitting zero because it's decremented by only one each iteration)

3. This question again discusses the Fibonacci numbers, where (as stated in question 2),

F(0) = 0
F(1) = 1
For iZ, where i>=2, F(i) = F(i-1) + F(i-2)

The beginning of the sequence looks like this:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

Note that every third element of the sequence is even.

Use induction to prove this, i.e. that F(i) is a multiple of 2 iff i is a multiple of 3.

Solution:

Theorem: For any i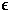N, F(3i) is even, and F(3i+1) and F(3i+2) are odd.

Proof:

Here I'm assuming that we know that the sum of two even numbers is even, the sum of two odd numbers is even, and the sum of an odd plus an even number is odd. These could be (trivially) proved separately if desired.

Base case (i=0): Observe that F(0) is even, and F(1) and F(2) are odd.

Now, for any k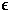N, assuming that the theorem holds for i=k, prove that the theorem holds for i=k+1.

So, we are assuming that F(3k) is even, F(3k+1) is odd, and F(3k+2) is odd.

And we need to prove that F(3k+3) is even, F(3k+4) is odd, and F(3k+5) is odd.

First, F(3k+3) is F(3k+1)+F(3k+2), which is an odd plus an odd, so F(3k+3) is even.

Next, F(3k+4) is F(3k+2)+F(3k+3), and we know that F(3k+2) is odd, and we've just shown that F(3k+3) is even, so F(3k+4) is odd.

Finally, F(3k+5) is F(3k+3)+F(3k+4), and we've just shown that F(3k+3) is even and F(3k+4) is odd, so F(3k+5) is odd.

(Obviously, there are many other possible ways to organize this proof, and also, I expect that student answers, given the test conditions and the time pressure, will be much more terse than the above.)